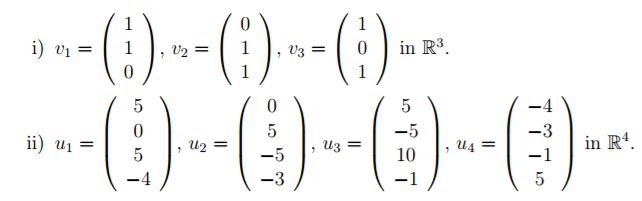Sind die Vektoren linear abhängig oder unabhängig?

Question

ich mach gerade diese Aufgabe. 

Bei der a) hab ich raus, dass die Vektoren linear unabhängig sind, da die Determinante D=2 ist.

Bei der b) hab jetzt dazu folgendes gemacht:

(5     0      5     -4                 *   (  Lamda1                = (0

 0      5     -5     -3                        Lamba2                    0

 5      -5     10    -1                       Lamba3                    0

-4      -3      -1     5)                      Lamba4)                   0)

Hab daraus jetzt ein LGS gemacht.

Nachdem ich die dritte Zeile mit 4 multipliziert habe und die vierte Zeile mit 5 und dann die 3 in die 4 addiert habe.

Hab ich dann die 2 mal 7 genommen und dann in die neue vier. Dann hatte ich eine Zeile 0 0 0 0 0, weshalb doch die Vektoren alle linear abhängig sind oder?

 

Answer 1

Ja, hast du alles richtig gemacht.  Scheint ein gutes neues Jahr zu geben.

Answer 2

III - I

5*IV + 4*I

[0, 5, -5, -3]
[0, -5, 5, 3]
[0, -15, 15, 9]

II + I
III + 3*I

[0, 0, 0, 0]
[0, 0, 0, 0]

Damit hast du 2 Freiheitsgrade

Damit sind die Vektoren linear abhängig.

Answer 3

Hallo Like,

sobald du mit den Gauß-Umformungen eine Nullzeile erhältst, ist die Menge der Spaltenvektoren linear abhängig, das ist richtig.

Gruß Wolfgang

Answer 4

Nun - das heißt zunächst mal, dass die vier Vektoren nicht linear unabhängig sind.

Der Umkehrschluss, dass alle (paarweise!) linear abhängig sind ist falsch, da ja offensichtlich \(u_1\) und \(u_2\) nicht linear abhängig sind. Wenn Du die Matrix weiter vereinfachst, so fällt noch eine weitere Zeile mit 0'en heraus. Dann bleiben zwei Zeilen übrig - die Matrix hat demzufolge den Rang 2. Anbei meine Rechnung:

Gruß Werner

Answer 5

zu (i) Annahme: Die Vektoren sind linar abhängig oder der Nullvektor ist auch nichttrivial erzeugbar (m.a.W.: es gibt k≠0, h≠0 und j≠0 sodass v₁·k+v₂·h+v₃·j=Nullvektor). Dann ergibt sich das LGS

k+j=0

k+h=0

h+j=0

Dies hat nur die triviale Lösung h=k=j=0. Die Vektoren sind linar unabhängig.