Rekonstruktion f dritten Grades mit Tiefpunkt (1 | -2) und Wendepunkt im Koordinatenursprung.

Question

ich habe eine Frage zur Rekonstruktion.

Und zwar lautet die Aufgabe:
a) Gesucht ist eine ganzrationale Funktion dritten Grades mit dem Tiefpunkt (1 | -2), deren Wendepunkt im Koordinatenursprung liegt.
b) Der Graph einer ganzrationalen Funktion dritten Grades hat im Ursprung und im Punkt P (2 | 4) jeweils ein Extremum.

Dritten Grades bedeutet ja: f(x) = a · x³ + b · x² + c · x + d
Und jetzt? Ich würde das gerne in meinen CAS Taschenrechner eingeben, weiß aber nicht wie ich weiter vorgehe soll...

Danke für die Antworten

Answer 1

Benutze die Seite www.arndt-bruenner.de/mathe/scripts/steckbrief.htm und folgende Bedingungen

a)

f(1) = -2

f'(-1) = 0

f(0) = 0

f''(0) = 0

b)

f(0) = 0

f'(0) = 0

f(2) = 4

f'(2) = 0

Comments

Die Gleichungen die der mathecoach angegeben hat, liefern auf der oben stehenden HP ganz geschmeidig:

Answer 2

Eine Funktionsgleichung dritte Grades lautet f(x)=a · x³ + b · x² + c · x + d . Erste Ableitung f '(x)=3ax²+2bx+c. Zweite Ableitung f ''(x)=6ax+2b. Hier die vom Mathecoach genannten Gegebenheiten eingesetzt;

a)

f(1) = -2     -2=a+b+c+d

f'(-1) = 0     0=3a-2b + c

f(0) = 0       0=d

f''(0) = 0      0=2b daher b=0

Zu lösen bleibt noch

-2=a+c

0=3a+c

Das geht ohne CAS schneller im Kopf.

Answer 3

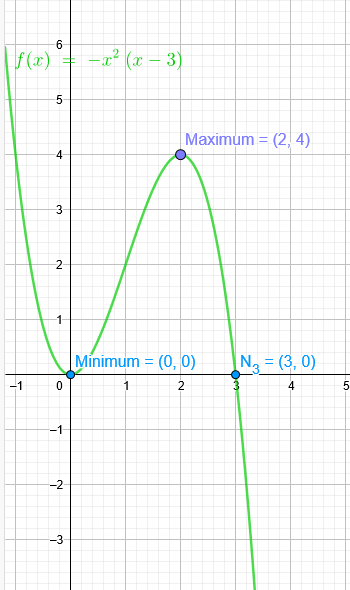
"b) Der Graph einer ganzrationalen Funktion dritten Grades hat im Ursprung und im Punkt P (2 | 4) jeweils ein Extremum."

Weg über die Nullstellenform der kubischen Parabel:

f(x)=a(x-N_1)(x-N_2)(x-N_3)

Extremum im Ursprung (doppelte Nullstelle):

f(x)=a*x^2*(x-N_3)

Punkt P (2 | 4)

f(2)=a*4*(2-N_3)

a*4*(2-N_3)=4      →      a*(2-N_3)=1   →    a=\( \frac{1}{2-N_3} \)

f(x)=  \( \frac{1}{2-N_3} \) *x^2*(x-N_3)

Extremwerteigenschaft bei x=2:

f´(x)=  \( \frac{1}{2-N_3} \)[ 2x*(x-N_3)+x^2]

f´(2)=  \( \frac{1}{2-N_3} \)[ 4*(2-N_3)+4]

\( \frac{1}{2-N_3} \)[ 4*(2-N_3)+4]=0

4*(2-N_3)+4=0    →   2-N_3+1=0     →   N_3=3

f(x)= -x^2*(x-3)