Hi,
zu lösen sind die Gleichungen
$$ (1) \quad \frac{\partial}{\partial a_i} F(a,b) = 0 \text{ für } i \ge 1 $$
$$ (2) \quad \frac{\partial}{\partial b_i} F(a,b) = 0 \text{ für } i \ge 1 $$
$$ (3) \quad \frac{\partial}{\partial b_0} F(a,b) = 0 $$
Die partiellen Ableitungen berechnen sich zu
$$ (4) \quad \frac{\partial}{\partial a_i} F(a,b) = -2i \omega \int_0^P \left[ f(x) - t_n(x) \right] \cos(i \omega x)\ dx = 0 $$
$$ (5) \quad \frac{\partial}{\partial b_i} F(a,b) = -2i \omega \int_0^P \left[ f(x) - t_n(x) \right] \sin(i \omega x)\ dx = 0 $$
$$ (6) \quad \frac{\partial}{\partial a_0} F(a,b) = -2i \omega \int_0^P \left[ f(x) - t_n(x) \right] dx = 0 $$
Die Gleichungen (4) - (6) ergeben mit den Hinweisen
$$ (7) \quad a_k = \frac{2}{P} \int_0^P f(x) \cos(k \omega x) \ dx $$
$$ (8) \quad a_k = \frac{2}{P} \int_0^P f(x) \sin(k \omega x) \ dx $$
$$ (9) \quad a_0 = \frac{1}{P} \int_0^P f(x) \ dx $$
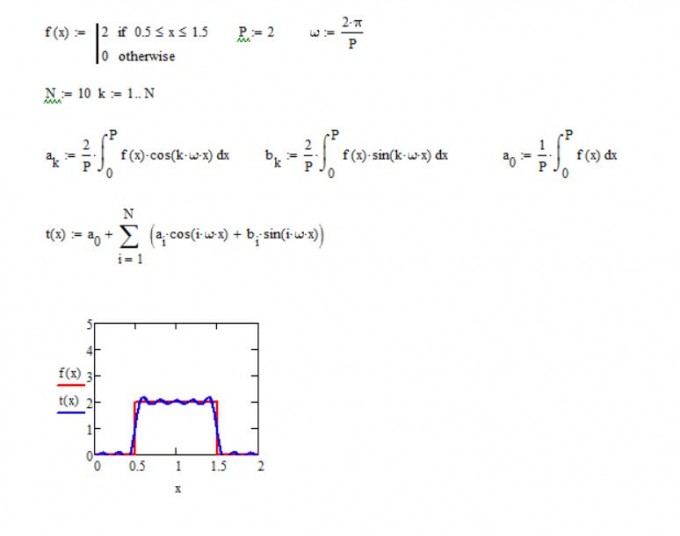
Als Beispiel schau Dir diese Funktion an