Ich unterstelle mal, dass die Bezeichnung der Seiten und Winkel in der üblichen Art und Weise erfolgt ist. Dann ergibt sich folgendes Bild
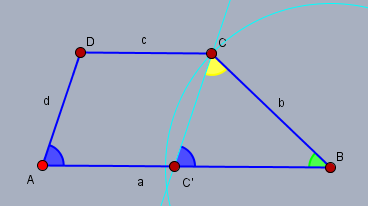
ich habe noch einen Punkt C' hinzugefügt, der die Punkte C, D und A zu einem Parallelogramm ergänzt. Der blaue Winkel ist das \(\alpha\). Der Weg zur Lösung der Aufgabe führt über das Dreieck C'BC. Die Strecke C'B ist die Differenz \(a-c\). Mit Hilfe des Sinussatzes lässt sich dann der Winkel C'CB (gelb) berechnen $$\frac{\sin C'CB}{a-c}=\frac{\sin \alpha}{b} \quad \Rightarrow C'CB=\arcsin {\frac{(a-c)\sin \alpha}{b}} \approx 64,62°$$ Über die Winkelsumme im Dreieck erhält man dann den Winkel \(\beta\) (grün). $$\beta = 180 - \alpha - C'CB \approx 43,38°$$ und mit dessen Hilfe dann die Höhe \(h\) $$\frac{h}{b}=\sin \beta \quad \Rightarrow h = b \cdot \sin \beta \approx 4 \text{cm} \cdot \sin 43,38° \approx 2,75 \text{cm}$$ Die Fläche des Trapez ist $$F=\frac{1}{2}(a+c)\cdot h\approx\frac{1}{2}(7 \text{cm} + 3,2 \text{cm}) \cdot 2,75 \text{cm} =14,025 \text{cm}^2$$ Die Seite \(d\) folgt aus der Höhe \(h\) und dem Winkel \(\alpha\) $$\frac{h}{d}=\sin \alpha \quad \Rightarrow d=\frac{h}{\sin \alpha} \approx \frac{2,75 \text{cm}}{ \sin{72°}} \approx 2,89 \text{cm}$$ Die restlichenWinkel sollten jetzt kein Problem mehr darstellen (\(\gamma \approx 136,6°\), \(\delta = 108°\))
Gruß Werner