Du kannst alle Punkte unter Aufgabe 10 auf wenige Informationen zurückführen. Betrachte dazu den Einheitskreis, in den ich den Winkel von +30° (blau) eingezeichnet habe:
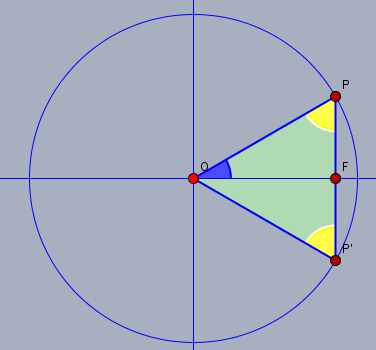
Der gegenüberliegen Winkel in P (gelb) ist demnach 60°, was aus der Winkelsumme im Dreieck OFP folgt. Nun spiegele ich P an der X-Achse zu P' und erhalte das gleichseitige Dreieck OPP'. Gleichseitig deshalb, weil alle Winkel identisch zu 60° sind. Da die Strecke OP immer =1 ist (Einheitskreis) muss PF zwangsläufig \(\frac{1}{2}\) sein. Die Strecke PF entspricht aber auch \(\sin 30°=\sin \frac{\pi}{6}=\frac{1}{2}\).
Der \(\cos 30°=\cos \frac{\pi}{6}\) entspricht der Strecke OF und lässt sich über den Pythagoras im rechtwinkligen Dreieck OFP berechnen. $$\cos 30°=\cos \frac{\pi}{6}=OF=\sqrt{1-\left( \frac{1}{2}\right)^2 }=\frac{1}{2}\sqrt{3}$$ Überhaupt gilt für jeden(!) Winkel \(\phi\) $$\sin^2 \phi + \cos^2 \phi=1$$
a) jetzt nur einsetzen: $$\sin 30° + \cos^2 30°= \frac{1}{2} + \left( \frac{1}{2} \sqrt{3}\right)^2= \frac{5}{4}$$
b) hier kommt jetzt eine neue Sache hinzu: Es gilt auch immer \(\cos \phi = \sin{(90°-\phi)} = \sin{(\frac{\pi}{2}-\phi)}\), was sich leicht an einem beliebigen rechtwinkligen Dreieck überprüfen lässt. Das der \(\tan \phi = \frac{\sin \phi}{\cos\phi}\) ist sollte bekannt sein. Demnach ist hier $$\tan \frac{\pi}{6} + \cos \frac{\pi}{3}=\frac{\sin \frac{\pi}{6}}{\cos \frac{\pi}{6}} + \sin {(\frac{\pi}{2} - \frac{\pi}{3})}=\sin \frac{\pi}{6} \left( \frac{1}{\cos \frac{\pi}{6}} + 1\right) = \frac{1}{2}\left( \frac{2}{\sqrt{3}}+1 \right)=\frac{1}{6}(2\sqrt{3} + 3)$$
c) nimm hier die 3.binomische Formel $$\sin^4 60° - \cos^4 60°=(\sin^2 60° + \cos^2 60°)(\sin^2 60° - \cos^2 60°)$$ .. und den Rest schaffst Du alleine, wenn Du weißt, dass auch \(\sin \phi = \cos{(\frac{\pi}{2}-\phi)}\) ist (s.o.)
d) nimm beide Faktoren unter eine gemeinsame Wurzel $$\sqrt{1 + \cos 30°} \sqrt{1 - \cos 30°}= \sqrt{(1 + \cos 30°)(1 - \cos 30°)}=\sqrt{1 - \cos^2 30°}$$ und das hatten wir auch schon (s.o.)
Gruß Werner