Ich nehme mal an, dass sich die Straße an zwei benachbarten Seiten des Grundstücks befindet; d.h. es liegt ein Eckgrundstück vor. Dann sieht das ganze so aus:
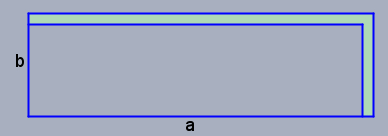
Das ursprüngliche Grundstück habe die Abmessungen \(a\) und \(b\). Dann gilt $$a \cdot b = 1080 \text{m}^2$$ Der Radweg besteht aus zwei Stücken \(2\text{m} \cdot a\) und \(2\text{m} \cdot (b-2\text{m})\). Beim zweiten Stück muss man von \(b\) 2m abziehen, da dies bereits vom ersten Teil vereinnahmt wird. Die Fläche des Radweges ist ebenfalls gegeben $$2\text{m} \cdot a + 2\text{m} \cdot (b-2\text{m}) =152\text{m}^2$$ Daraus folgt: $$a + b - 2\text{m}=76\text{m} \quad \Rightarrow b = 78\text{m}-a$$ Einsetzen in die erste Gleichung ergibt $$a \cdot (78\text{m}-a) = 1080 \text{m}^2$$ $$a\cdot 78 \text{m} -a^2=1080 \text{m}^2$$ $$a^2 - a\cdot 78 \text{m} +1080 \text{m}^2=0$$ $$a_{1,2}=39 \text{m} \pm \sqrt{39^2 \text{m}^2 - 1080 \text{m}^2} \quad \Rightarrow a_1=60 \text{m}; \quad a_2=18 \text{m}$$ und das sind auch gleichzeitig die Abmessungen des ursprünglichen Grundstücks.
Gruß Werner