Im Allgemeinen ist dann für das Rechteck noch eine weitere Information gegeben. Sonst gibt es - wie Roland bereits erwähnte - unendlich viele Möglichkeiten für das resultierende Rechteck.
Sollte eine Seite des Rechtecks gegeben (hier \(UV\)) sein und diese ist länger als die Seite des Quadrat, so schlage um den Punkt \(A\) des Quadrats einen Kreis mit dem Radius \(UV\), der \(BC\) bzw. dessen Verlängerung in \(P\) schneidet.
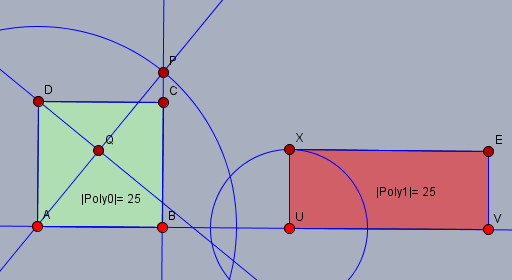
Konstruiere die Senkrechte von \(D\) auf die Gerade durch \(A\) und \(P\) mit dem Fußpunkt \(Q\). Die Strecke \(DQ\) ist die Länge der kürzeren Seite des flächengleichen Rechtecks.
Sollte die gegebene Seite kürzer sein, so ist die Konstruktion ähnlich - nur 'rückwärts': Konstruiere den Thaleskreis über \(DA\) und schlage um \(D\) einen Kreis mit dem Radius der kürzeren Seite (z.B. \(UX\)), der den Thaleskreis in \(Q\) schneidet. Die Gerade durch \(A\) und \(Q\) schneidet \(BC\) oder dessen Verlängerung in \(P\). Der Abstand zwischen \(A\) und \(P\) ist die Länge der längeren Seite.
Gruß Werner