Gegeben: Zeichenfolge: D B A E C D E A B D F A C E A D D E C B E A D F C G D E A D E B C D E
Ermitteln Sie für den aufgeführten Text eine Code-Tabelle nach dem HuffmanVerfahren durch Bestimmung des Code-Baumes. Komprimieren Sie die ersten fünf (5) Zeichen des Textes mit der von Ihnen bestimmten Code-Tabelle.
Sie haben nun die Aufgabe einen Text, bestehend aus 150.000 Zeichen, mit dem von Ihnen ermittelten Code zu kodieren. Wieviel Platz werden Sie in etwa einsparen, wenn Sie das Ergebnis mit einem Fixed Length Code minimaler Länge kodieren?
(ca. Länge Huffmann, Länge Fixed Length, Einsparung in %)
________________________________________________
A = 6, B = 4, C=5, D = 9, E = 8, F=2, G=1, Spaces = 34
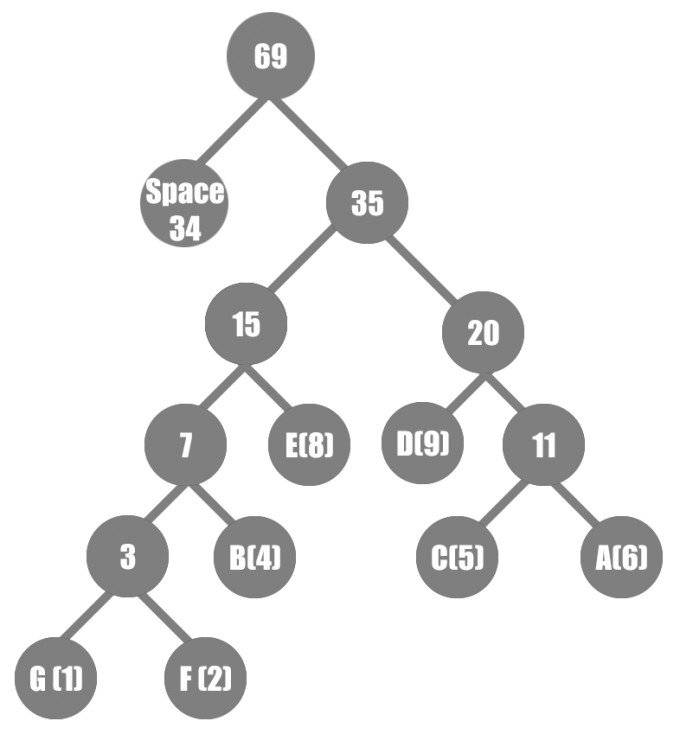
Sieht mein Baum richtig aus?
A = 1111, B = 1001, C=1110, D = 110, E = 101, F=10001, G=10000, Spaces = 0
________________________________________________
"Komprimieren Sie die ersten fünf (5) Zeichen des Textes mit der von Ihnen bestimmten Code-Tabelle."
Ist damit "D B A" gemeint?
"D B A" = 1100100101111
Wie berechne ich die Ersparnis? [ 1 - (neue Codelänge) / (alte Codelänge)] ? Doch was ist die Alte Codelänge?
Ist die neue Codelänge die Länge des Zeichens mit der kleinsten Wahrscheinlichkeit?
G kommt einmal dran (G=10000) == Neue Codelänge = 5?