Question

f(x) = -x^2 + sin(2x) + π. Was kann man über dieses ξ aussagen?


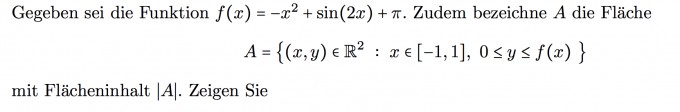
Die Aufgabe lautet : "Zeigen Sie, es existiert ein ξ, sodass 2f(ξ) = |A|. Was kann man über dieses ξ aussagen?"

Alles worauf ich komme ist: An der Stelle ξ hat die funktion f den Wert |A|/2.
Das ist natürlich super offensichtlich aber mir fällt sonst nichts ein. Kann mir jemand bitte weiterhelfen?

Danke.

Comments

Das ξ könnte zwischen -1 und 1 liegen.

Hast du eine Skizze? Hat f(x) im fraglichen Intervall eine Nullstelle?

https://de.wikipedia.org/wiki/Mittelwertsatz_der_Integralrechnung 

---

Keine Skizze. f(x) hat Nullstellen aber nicht in [-1,1].

---

identische Originalfrage

https://www.mathelounge.de/415080/integralrechnung-gegeben-sei-die-funktion-f-x-%E2%88%92x-2-sin-2x-%CF%80

---

Danke für die Verlinkung. Schliessen kann ich keine von beiden, da im Original mehr Teilfragen gestellt wurden.

Answer 1

Du kennst vielleicht die Formel für den

Mittelwert einer Funktion über einem Intervall [a;b]


m =  1 / (b-a) * Integral von a bis b über f(x) dx.


Das wäre ja hier m = 1/2 * |A|.  Hier etwa 2,8
Also ξ ≈ -0,2 denn  der Graph sieht ja so aus:


 ~plot~ -x^2 +sin(2x) +pi ~plot~