Monotonie wie geht das genau?

Question

ich habe eine Frage zur Monotonie. Wie sieht man was es ist? Ich weiß, dass die Funktion steigend oder fallend monoton sein kann. Aber ich weiß nicht wie ich sehen kann ob es so ist. Wenn ich jetzt durch ausrechnen der Extremstellen -2,0 und 2 (mit f´(x)=0  )raushabe, wie sehe ich dann ob die Funktion von oben (dann streng monoton fallen? ) bzw. von unten ( dann streng monoton steigend ?) kommt? Ich habe ja nur die x- Werte von den Extremstellen(für Extremstellen wird doch nur die erste Abletung 0 gesetzt oder liegt da schon der Fehler?). Ich hoffe ihr könnt mir helfen, das Internet konnte es bis jetzt nicht :/

Vielen Dank fürs ansehen.

Answer 1

Am Besten du hättest die Funktion auch angegeben.

Stellen mit waagerechter Tangent ( Extremstellen;
Sattelpunkte )
f ´( x ) = 0

Monotonie steigend
f ´( x ) > 0

Monotonie fallend
f ´( x ) < 0

Comments

Also die Funktion lautet: f(x)=x⁴-8x²+16, x∈ℝ die soll auf Monotonie untersucht werden und die Extremstellen sollen bestimmt werden auf dem vorgegebenen Definitionsbereich.

so meine Ableitung war dann f´(x)=4x³-16x. f´(x)=0 dann habe ich die Extremstellen von -2;0;2 raus. Für die Untersuchung der Monotonie nehmen ich dann die Ursprungsgleich oder die Ableitung? Ich weiß irgendwie nicht woran ich sehe ob sie fallend am Anfang ist also von oben kommt oder steigend und dann von unten kommt. Oder ist das egal aus welcher Richtung sie Anfangs kommt. Ich weiß auch dass sie von -∞ über -2, 0 , 2 zu +∞ geht

---

f´(x)=4x³-16x.

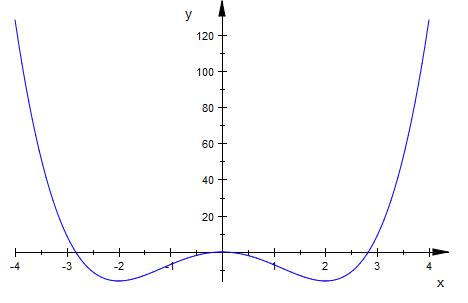
f = x^4 - 8 * x^2
f ´( x ) = 4 * x^3 - 16 * x
f ´´ ( x ) = 12 * x^2 - 16

Stellen mit waagerechter Tangente
f ´( x ) = 0
x = -2
x = 0
x = 2

Monotonie > 0 ( steigend )
4 * x^3 - 16 * x > 0
x * ( 4 * x^2 - 16 ) > 0

1.Fall
x > 0 und
4 * x^2 - 16 > 0
x^2 > 4
x > 2
und x < -2

( x > 0 ) und ( x > 2 )  => x > 2
( x > 0 ) und ( x -2 )  => keine Schnittmenge

2.Fall
x < 0 und
4 * x^2 - 16 < 0
x^2 < 4
-2 < x < 2
( x < 0 ) und ( -2 < x < 2 )  => -2 < x < 0

Def-Bereich : keine Einschränkungen

Monotonie
-∞ .. -2  : noch nicht  bekannt
-2 : null
-2 .. 0 steigend
0 : null
0..2 : noch nicht bekannt
2 : null
2 .. ∞ : steigend

Es könnten jetzt noch jetzt noch die
Nachweise für
f ´( x ) < 0 ( fallend ) geführt werden.
Das überlasse ich einmal dir.

Soviel zunächst.

Answer 2

> Wenn ich jetzt durch ausrechnen der Extremstellen -2,0 und 2 (mit f´(x)=0  ) raushabe

Berechne an je einer Stelle aus den Intervallen (--∞; 2), (2; 0), (0; 2) und (2; ∞) die Ableitung. Ist sie positiv, dann ist die Funktion auf diesem Intervall streng monoton steigend, andernfalls ist sie stregn monoton fallend.

Das funktioniert, wenn der maximale Definitionsbereich der Funktion ℝ ist und die Funktion überall differenzierbar ist. Bei ganzrationalen  Funktionen ist das der Fall.