Question

Simplex Grafische Lösung   
10_x1-2_x2 ≥30   und 10_x1+3_{x2≤100   nach x2} auflösen und ins Koordinatensystem einzeichnen

Comments

"ähnliche Frage": https://www.mathelounge.de/415836/lineare-optimierung-graphisch-maximiere-nebenbedingungen

Answer 1

ich schreibe  y = x₂  und   x  = x₁     und    gehe von  x,y ≥ 0  aus.   #  

10x - 2y ≥ 30   und   10 x + 3y ≤ 100

⇔  y ≤ 5·x - 15   und    y ≤ - 10/3·x + 100/3   

Zeichne die beiden zugehötigen Geraden   y = 5·x - 15   und    y =  - 10/3·x + 100/3

Die Lösungsmenge sind die Punkte in dem Dreieck (einschließlich der Randlinien) im 1. Quadranten die unterhalb der ersten und der zweiten Geraden liegen.

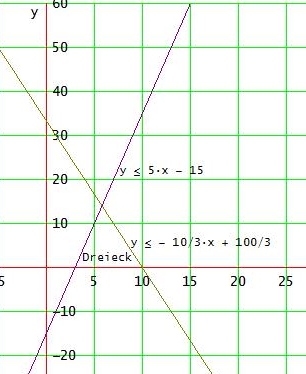
#  wenn nicht (x,y ≥0) , setzt sich die Fläche unterhalb der x-Achse fort.

Gruß Wolfgang

Answer 2

Leider ist meine erste Antwort verschwunden.

Alles oberhalb von blau.
Alles unterhalb von rot.