Ich nutze zur Beantwortung einmal die Diff-Rechnung.
Die Normalparabel p1 hat die Funktionsgleichung y = x2 + 6x + 7.
a) Berechnen Sie die Koordinaten des Scheitelpunktes S1 der Parabel p1.
f ( x ) = x^2 + 6x + 7
f ´( x ) = 2x + 6
2x + 6 = 0
x = -3
f ( -3 ) = 9 - 18 + 7 = -2
S ( -3 | -2 )
b) Die Punkte P1 (-3 / 2) und P2 (1 / -6) liegen auf dem Graphen eines nach unten geöffneten Normalparabel p2. Ermitteln Sie rechnerisch die Funktionsgleichung in Normalform.
g ( x ) = -x^2 + b * x + c
g ( -3 ) = -9 - 3b + c = 2
g ( 1 ) = -1 + b + c = -6
-9 - 3b + c = 2
-1 + b + c = -6
2 Gleichungen mit 2 Unbekannten
g ( x ) = -x^2 - 4*x - 1
c) Bestimmen Sie rechnerisch die Koordinaten des Scheitelpunktes S2 der Parabel p2.
g ´( x ) = -2x - 4
-2x - 4 = 0
x = -2
g ( -2 ) = 3
S ( -2 | 3 )
d) Zeichnen Sie die Graphen von p1 und p2 in ein Koordinatensystem mit der Längeneinheit 1cm.
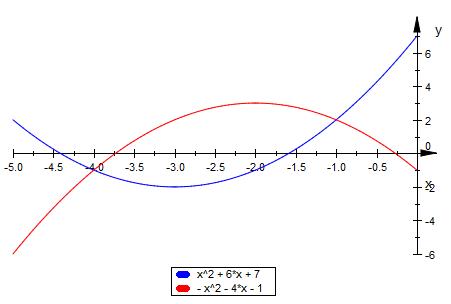
e) Berechnen Sie die Koordinaten der Schnittpunkte T1 und T2 der beiden Parabeln p1 und p2. (Rechnen sie mit p2: y = -x2 - 4x -1)
f ( x ) = g ( x )
x^2 + 6x + 7 = -x^2 - 4*x - 1
Kannst du das ?
x = - 4
x = -1