Lineare Optimierung: Wieviele Tage jede Grube pro Woche befahren, um Aufträge zu erfüllen? Bergwerksgesellschaft

Question

Aufgabe:

Eine Bergwerksgesellschaft besitzt zwei verschiedene Gruben (bzw. Minen), in denen bestimmte Erzarten gefördert werden. Die Gruben befinden sich in verschiedenen Landesteilen und verfïgen ūber unterschiedliche Kapazitāten. Beim Brechen ergeben sich die drei Sorten grob-, mittel- und feinkōrniges Erz. Nach joder Erzwarte besteht eine gewisse Nachfrage. Die Bergwerksgesellschaft koazentriert sich darauf, einem Hüttenwerk wöchentlich mindestens \( 12 \mathrm{t} \) (Tonnen) grob-, \( 8 \mathrm{t} \) mittel- und 24 t feinkörniges Erz zu liefern.

Die Betriebskosten für die Gruben sind 200 GE pro Tag bei Grube 1 und 160 GE bei Grube 2. In der Grube 1 werden dabei pro Tag \( 6 t \) grob-, \( 2 t \) mittel- und \( 4 t \) feinkörniges Erz gefơrdert, während die zweite Grube eine tägliche Leistung von \( 2 \mathrm{t} \) grob-, \( 2 t \) mittel- und \( 12 t \) feinkörnigem Erz hat.

Wieviele Tage sollte jede der Gruben pro Woche befahren werden, um die Aufträge der Firma auf wirtschaftliche Weise zu erfüllen?

Answer 1

6x + 2y ≥ 12
y ≥ 6 - 3x

2x + 2y ≥ 8
y ≥ 4 - x

4x + 12y ≥ 24
y ≥ 2 - x/3

K = 200x + 160y --> Soll minimiert werden
y = K/160 - 200/160*x = K/160 - 5/4*x

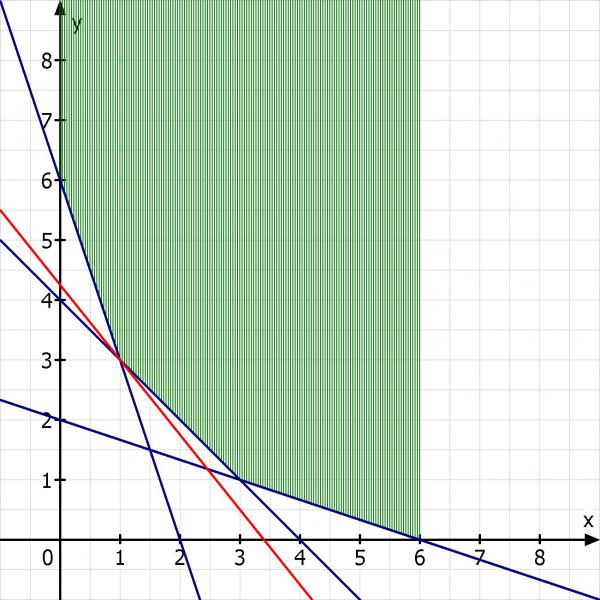
Ich zeichne die oberen 3 Gleichungen in ein Koordinatensystem ein

Dann zeichne ich mir die Isokostengerade in den Punkt, der gerade nur noch eine Lösung erlaubt das ist dann die kleinste Lösung.

Die Lösung wäre hier x = 1 und y = 3

Grupe 1 sollte also 1 mal pro Woche und Grube 3 sollte 3 mal pro Woche befahren werden. Mit der Simplex Methode kannst du es auch rechnen und dann dein Simplex Tableau hier reinstellen, dann kontrollieren wir das Gerne. Du solltest aber auf die gleiche Lösung kommen.

Ich habe es bewusst mit einer Methode der 8. bzw. 9 Klasse gelöst, damit mehr Leute von dieser Lösung profitieren.

Skizze: