Wie berechne ich das Produkte mit einem Isomorphismus Z7 x Z11 z13

Question

Gegeben ist der Isomorphismus Z1001 -> Z7 x Z11 z13

Hierin soll ich das Produkt der Zahlen 32 und 14 bilden. Leider weiß ich nicht, wie ich da ansetzen soll.

Answer 1

Guten Morgen MathFox, 

wir betrachten also den Isomorphismus: $$\mathbb{Z}_{1001}\rightarrow\mathbb{Z}_{7}\times \mathbb{Z}_{11}\times \mathbb{Z}_{13}$$ Um damit rechnen zu können, bringen wir die Faktoren in eine dafür geeignete Form und berechnen so das Produkt: 

Dieses Ergebnis muss nun wieder in $$\mathbb{Z_{1001}}$$ zurückgerechnet werden. Dazu verwenden wir das Chinese Remainder Theorem (CRT). Wir beginnen mit dem Aufstellen des Systems Linearer Kongruenzen: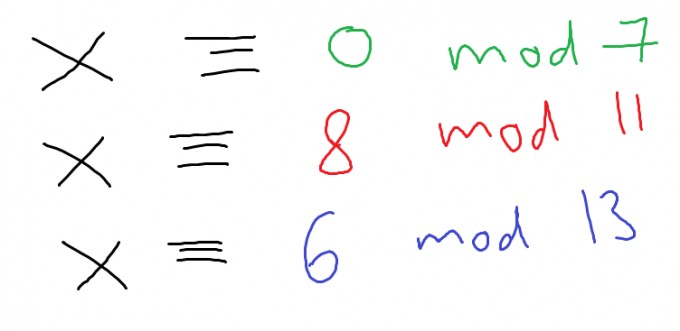 

Durch schrittweises Anwenden des CRT erhalten wir folgenden Wert für x, der bezüglich des Moduls 1001 eindeutig ist: $$x\equiv 448\mod 1001$$

Von der Richtigkeit dieses Ergebnisses überzeugen wir uns, indem wir direkt in $$\mathbb{Z}_{1001}$$ das gesuchte Produkt berechnen: $$32\cdot 14=448\mod 1001$$

Wenn Du etwas nicht verstehen solltest, kannst Du Dich gerne wieder melden! 

André, savest8