Wie lässt sich diese Gleichung lösen? 8^x - 9x^2 + 12x - x = 3612

Question

ich wollte Fragen, ob es eine Möglichkeit gibt, die oben angeführte Gleichung zu lösen, bzw. wie eben die Ansätze zur Lösung einer solchen aussehen würden?

Vielen Dank für jede Hilfe.

Answer 1

 
es handelt sich bei $$ 8^x - 9x^2 + 12x - x = 3612$$ um eine transzendente (nicht algebraische) Gleichung, d.h. Du kannst x nicht mit elementaren Ausdrücken darstellen. Einen Beweis für meine Aussage liefert WolframAlpha: https://www.wolframalpha.com/input/?i=8%5Ex+-+9x%5E2+%2B+12x+-+x+%3D+3612. 
Die Lösung ist jedoch approximierbar. Hierfür kannst Du z.B. das Newton-Verfahren verwenden. Die Genauigkeit des Ergebnisses hängt dabei von der Anzahl der Iterationen ab. Ein gutes Video zum Newtonschen Näherungverfahren gibt es hier:

Wenn Du Rückfragen hast, dann stelle sie gerne!
André, savest8

Answer 2

das ist eine transzendente Gleichung, man kann also nach x nicht mit elementaren Funktion auflösen.

Lösen kannst du die Gleichung mit Näherungsverfahren wie dem Newtonverfahren.

Das ergibt dann x≈ 3.9569

Answer 3

Wäre nicht der Quadratische Anteil ( 9x² ), könnte man es so lösen (Beispiel §5):

http://www.lamprechts.de/gerd/LambertW-Beispiele.html

Und bekäme auch noch komplexe Lösungen dazu.

Aber mit diesem 2-fach-nichtlinear-Anteil geht es nur numerisch. Der Iterationsrecher kann es per Newton:

Null-Funktion: pow(8,x)-9*x*x+12*x-x-3612  {wobei man auch 12x-1x=11*x }

Nur 4 Schritte für 15 richtige Nachkommastellen.

Oder per Bisektion

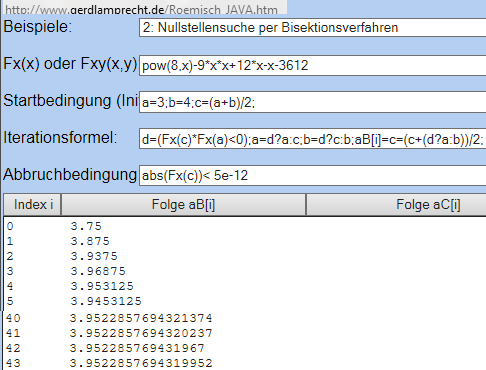
lösen . Vorsicht: wenn Abbruchbedingung zu klein, wird das Ziel nie erreicht -> Endlosschleife.

Weiterer Nachteil: 43 Schritte für gleiche Genauigkeit nötig.

Interessant ist, dass der Bruch 125207237598229 / 31679702557597

26 richtige Nachkommastellen liefert, aber mit dem richtigen Ergebnis

3.9522857694319950301940298290087617749825306418000635766236901899369948175718461679365847851239707...

nichts zu tun hat.