Zeigen Sie, dass sich die Ebenen E in Koordinatenform durch die Gleichung E: 12x + 2y + 11z -1 = 0 darstellen lässt.

Question

Aufgabe:

Das Parallelogramm ABCD A (6; 3; -7) B (0; 6; -1) C (-3; 2; 3) D (3; -1; -3) liegt in einer Ebene E in Parameterform an. Zeigen Sie, dass sich die Ebenen E in Koordinatenform durch die Gleichung E: 12x + 2y + 11z -1 = 0 darstellen lässt.

Problem/Ansatz:

AlsParameterform habe ich:

E: \( \vec{x} \) = \( \begin{pmatrix} 6\\3\\-7 \end{pmatrix} \) + s \( \begin{pmatrix} -6\\3\\6 \end{pmatrix} \) + t \( \begin{pmatrix} -9\\-1\\10 \end{pmatrix} \)

Nach dem bilden des Kreuzproduktes habe ich für  \( \vec{n} \) = \( \begin{pmatrix} 12\\2\\11 \end{pmatrix} \) heraus, was schon mal der Gleichung ähnelt. Wenn ich jetzt zum Beispiel den Punkt B in die oben gegebene Gleichung einsetze hätte ich:

E: 12*0 + 2*6 + 11*(-1) -1 = 0

E: 0 + 12 - 11 -1 = 0

E: 0 = 0

Kann ich das so darstellen?

Answer 1

Hallo Celine,

Kann ich das so darstellen?

Ja - das kannst Du.

wenn aber nicht ausdrücklich nach der Parameterform der Ebene gefragt ist, so muss die hier nicht berechnet und umgewandelt werden. Es ist ausreichend, zu prüfen, ob die einzelnen Punkte in der Ebene liegen. Dazu müssen sie die Ebenengleichung erfüllen.

Zum Beispiel für \(A\):$$A = \begin{pmatrix}6\\ 3\\ -7\end{pmatrix} \\ 12 \cdot 6 + 2\cdot 3 + 11\cdot (-7) - 1 = 0 \space \checkmark$$\(A\) liegt also in der Ebene und die anderen vier Punkte auch. Also deckt sich jede Parameterform der Ebene, die aus den vier Punkten bestimmt wird, mit der gegebenen Ebene \(E\).

Folgende Szene zeigt, dass die Punkte in der Ebene liegen.

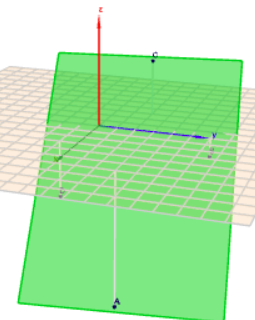
(klick auf das Bild, dann öffnet sich Geoknecht-3D und rotiere die Szene mit der Maus)

Gruß Werner