MathFox,
um diese Aufgabe zu lösen, benötigst Du eine "Entschlüsselungsfunktion". In diesem Fall ist das die inverse Permutation \(\pi^{-1}\) von \(\pi\).
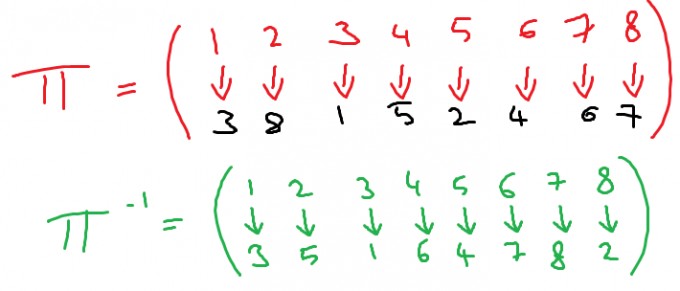
Nun nimmst Du den Geheimtext und vertauschst entsprechend der inversen Permutation die Buchstaben, also $$c(\pi^{-1}(1))=c(3)=C$$ $$c(\pi^{-1}(2))=c(5)=D$$ $$c(\pi^{-1}(3))=c(1)=A$$ $$c(\pi^{-1}(4))=c(6)=E$$ $$c(\pi^{-1}(5))=c(4)=D$$ $$c(\pi^{-1}(6))=c(7)=F$$ $$c(\pi^{-1}(7))=c(8)=A$$ $$c(\pi^{-1}(8))=c(2)=B$$ Der Klartext lautet also CDAEDFAB.
Und ja, man kann diese Aufgabe lösen. Es ist nämlich jede Permutation invertierbar. Zudem entspricht die Chiffrat-Länge der "Permutationslänge" (hier 8).
Konnte ich Dir damit weiterhelfen?
André, savest8