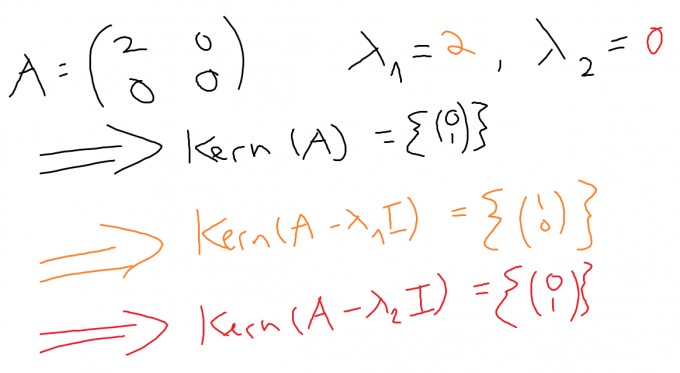zeigen, dass y=0 ein eigenwert von A ist

Question

angenommen man hat eine quadratische Matrix und soll zeigen, dass zum Beispiel y=1 ein Eigenwert dieser Matrix ist. Man kennt den dazugehörigen Eigenvektor noch nicht. 

Wie würde man das allgemein machen bzw. was muss gelten?

Answer 1

Hallo Simon_W 1997, 

Du berechnest das charakteristische Polynom der quadratischen Matrix und setzt den Eigenwert \(y=1\) ein. Wenn das Ergebnis 0 ist, handelt es sich um einen Eigenwert der Matrix.

Reicht Dir das als Erklärung oder möchtest Du noch ein Beispiel dazu haben?

André, savest8

Comments

Ja das habe ich verstanden. Aber geht das nicht schneller ohne Polynom? Denn in dieser Klausuraufgabe sollte man kein Charakter.  Polynom ausrechnen :)

---

Hallo Simon_W 1997, 

könntest Du vielleicht die Matrix aus der Aufgabenstellung posten?

Grüße

---

Noch eine Frage: welchen Wert hat der gegebene Eigenwert? Im Titel steht \(y=0\), in der Aufgabenbeschreibung \(y=1\).

---

Also das war eine ganz normale 3x3 matrix . Ich habe die Lösung leider nicht mehr da, aber da wurde irgendwie wie mit Kern gerechnet . Leider finde ich die Aufgabe nicht mehr :)

---

Wenn \(y=0\) ein Eigenwert der Matrix ist, dann ist diese nicht invertierbar. Wenn der Kern einen Vektor enthält (und dieser nicht trivial ist), dann ist die Matrix nicht invertierbar und \(y=0\) ein Eigenwert.

Hilft Dir das?

---

Ich schau mal ob ich die Aufgabe nochmal finde :) dann können wir das nochmal abarbeiten 

---

Okay. Das von mir zuvor beschriebene Kriterium gilt auf jeden Fall.

---

okay. Ich habe die Aufgabe bzw. die Lösung nochmal.Zeigen Sie: y=-1 ist ein Eigenwert von A.

---

Ich verstehe nicht, wie Kern(yI-A) =.... unabhängig von y sein kann

---

Einfacher wäre es in meinen Augen, wenn man die Determinante von \(\lambda\cdot I-A\) berechnet statt den Eigenvektor zu suchen, der noch nicht einmal gefordert ist. Aber gut, die werden sich schon etwas dabei gedacht haben;-) Die gehen davon aus, dass wenn Du den Kern von \(\lambda\cdot I-A\) berechnest und dieser einen nicht-trivialen Vektor \(v\neq 0\) enthält, \(\lambda\) ein Eigenwert ist, was ein durchaus legitimes Vorgehen darstellt. 
Was genau meinst Du mit "[...] wie Kern(yI-A) =.... unabhängig von y sein kann"? Das ist er ja nicht. Abhängig davon, welchen Wert \(\lambda\) annimmt, erhält man einen entsprechenden Eigenvektor. Hier ein kleines Beispiel: 

---

Wäre nicht nach dem Eigenvektor gefragt worden, hättest du dann eine Möglichkeit gesehen das anders zu lösen?

---

Gerne doch. Ja, ich hätte entweder \(A-\lambda\cdot I\) berechnet und geprüft, ob \(\det(A-\lambda\cdot I)=0\) (\(\lambda\) ist dann ein Eigenwert) oder das charakteristische Polynom \(p(x)\) zu \(A\) ermittelt und \(p(\lambda)=0\) geprüft (ähnlicher Gedanke wie bei der Determinante). Entwickelt hätte ich die Determinante nach der 3. Spalte, da man sich wegen \(a_{13}=0\) eine Unterdeterminante spart.