Lineares Optimierungsproblem - Ungleichung lösen - Simplex?

Question

ich bearbeite momentan folgende Aufgabe (Lösung steht dabei):

http://sos-mathe.ch/pdfg/g35_9.pdf

Das aufstellen der Nebenbedingungen sowie der Ziel-/Gewinnfunktion bekomme ich hin, ich verstehe leider überhaupt nicht wie man rechnerisch auf den Schnittpunkt (200/300) der beiden geraden kommt.

Kann man die Produktionsmengen auch mit dem Simplex-Algorithmus herausfinden? Ich kann diesen momentan nur bei Aufgaben anwenden bei denen eine Deckungsbeitragsfunktion ( zB. D(x) = 28x1 + 40x2 )  sowie die Restriktionen/Nebenbedingungen bereits gegeben sind, ich führe dazu dann noch die Schlupfvariablen ein und löse alles dann ganz normal. Ich weiß leider nicht wie ich das auf obige Aufgabe anwenden soll.

Zusammengefasst:

1. Wie kommt man auf den Schnittpunkt ohne Simplex?

2. Mit Simplex lösbar?

Vielen Dank und Grüße!

Comments

Nachtrag: 

Solche Simplexaufgaben kann ich mit meinem Wissen lösen:

Deckungsbeitragsfunktion und Restriktionen:

Starttableau:

Answer 1

Hier zunächst nochmals die Skizze

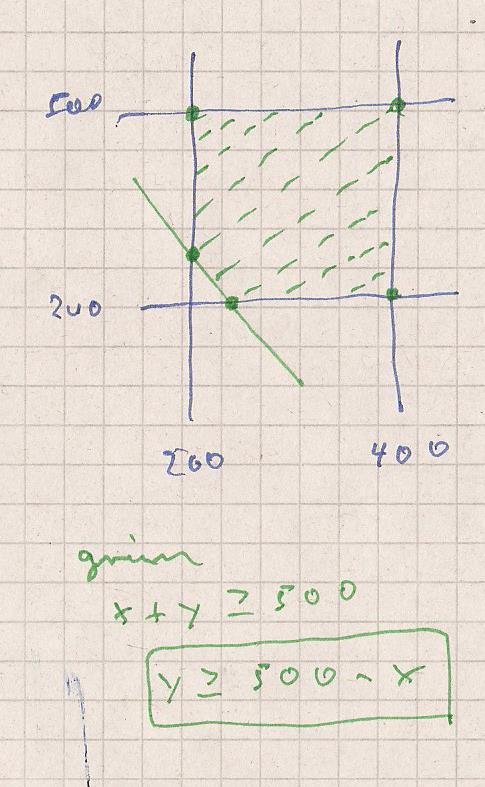
Die grüne Gerade ergibt sich wie oben hergeleitet.
Alles oberhalb der Geraden ( schraffierter Bereich )
gehört zu den möglichen Lösungen.

Für den Gewinn gilt
32000 - 30x - 25y soll einen maximalen Betrag ergeben.

32000 - 30x - 25y= max
Umgestellt als Geradengleichung ergibt sich
y = -30/ 25 * x + ( 32000 - max ) / 25

-30/25 ist die Steigung.Siehe dein Pdf. Unten die
kleine Gerade.

 ( 32000 - max ) / 25 ist der y-Achsenabschnitt
Da max möglichst groß werden soll
soll der y-Achsenabschnitt den geringsten Wert haben.
Das wird erreicht in dem die kleine untere Gerade
parallel ( unter Beibehaltung der Steigung ) nach oben
bis zum ersten Berührpunkt mit dem grünen Feld
verschoben wird.
Dies ist im Punkt E.

mfg Georg

Comments

Vielen Dank, das mit dem verschieben ist mir jetzt klargeworden, aber gibt es irgendeine rechnerische Möglichkeit auf die E(200/200) zu kommen?

---

Die Koordinaten aller Eckpunkte ermitteln
E ( 200 | 300 )
( 200 | 500 )
usw

Die Gerade ist die Funktion
y = -30/ 25 * x + b

Für Punkt E gilt
-30/ 25 * 200 + b = 300
b = 540

Wie oben geschildert ist der Eckpunkt
mit dem kleinsten b
- der Punkt mit dem größten max.