1. Einleitung
In den Sicherheitseinstellungen von Android hat man die Wahl zwischen verschiedenen Lock-Screen-Typen, die ein unterschiedlich hohes Maß an Sicherheit bieten. Als Schutzniveau-Metrik eignet sich beispielsweise die Anzahl an mathematischen Kombinationsmöglichkeiten, die theoretisch zur Umgehung des Schutzes durchprobiert werden müssten, wenn man die Passphrase nicht kennt. Wir werden in diesem Artikel herausfinden, weshalb die Sperrmuster nur einen mittleren Schutz bieten und die Wahl von PINs und Passwörtern eure Smartphones sicherer machen.
Bevor wir uns dem mathematischen Teil widmen, müssen die verschiedenen Schutzmechanismen verstanden werden:
Wischen - Beim Wischen wird das Smartphone durch einfaches Wischen über den Bildschirm entsperrt. Dass dies keinen Schutz bietet, bedarf keiner weiteren Erklärungen.
Sperrmuster - Ein Sperrmuster wird durch das Verbinden von Knoten in einem Graphen erzeugt. Um für unsere späteren Überlegungen ein geeignetes Modell zu haben, versehen wir die einzelnen Knoten mit Zahlen:

Der Anwender kann das Smartphone nur durch Eingabe des festgelegten Musters entsperren. Wie wir später sehen werden, muss ein solches Muster bestimmte Regeln erfüllen, welche die kombinatorische Betrachtung maßgeblich beeinflussen.
PIN - Ein PIN besteht aus mindestens \(4\) und maximal \(16\) Ziffern von \(0\) bis \(9\). An die einzelnen Stellen des \(4-\) bis \(16-\)stelligen Codes kann jede der \(10\) Ziffern treten. Es ergeben sich somit $$\sum_{k=4}^{16}10^k=11111111111110000$$ mögliche Codes.
Passwort - Im Vergleich zu den PINs setzen sich Passwörter nicht nur aus Ziffern, sondern aus dem gesamten zur Verfügung stehenden Zeichensatz zusammen. Die Passwortlängenregel ist dieselbe wie bei den PINs. Die Berechnung der Passwortmöglichkeiten basiert ebenfalls auf dem PIN-Ansatz, wobei die Basis des Exponenten die Anzahl des jeweiligen Zeichensatzes ist. Deshalb sind Passwörter weitaus sicherer, da mehr als \(10\) Zeichen pro Stelle genutzt werden können.
2. Das Problem
Die Frage ist, wie man die Anzahl an möglichen Sperrmustern berechnen kann. Wichtig ist dabei nicht nur das Muster, sondern auch die Art, auf die es erzeugt werden kann:
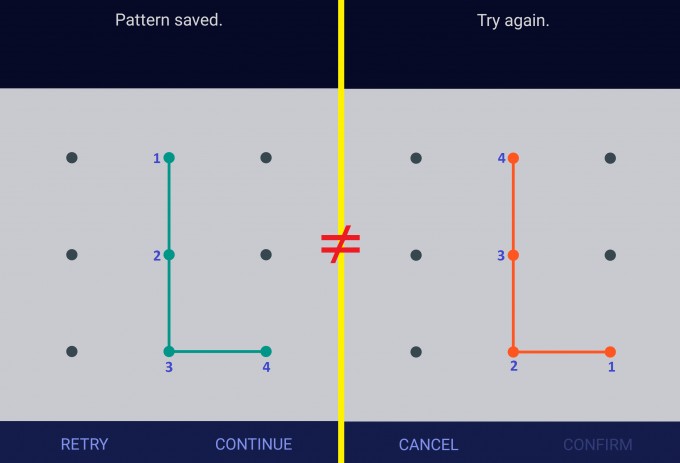
Zu beachten ist außerdem, dass das Muster folgende Regeln erfüllen muss:
- Ein Sperrmuster muss aus mindestens \(4\) und maximal \(9\) Knoten bestehen.
- Es sind keine „Sprünge“ erlaubt, d.h. die Folge \(1\rightarrow 3\rightarrow 7\rightarrow 4\) ist nicht möglich. Diese Regel gilt jedoch nicht, wenn ein zwischen zwei Knoten liegender Knoten bereits besucht wurde, d.h. die Kombination \(2\rightarrow 3\rightarrow 1\rightarrow 4\) kann als Sperre verwendet werden.
- Kein Knoten darf doppelt besucht werden.
3. Die Lösung
Wenn wir annehmen, dass nur die Längenregel Anwendung findet, ergeben sich $$\sum_{k=4}^{9}{\binom{9}{k}\cdot k!= 985824}$$ Möglichkeiten. Von dieser Anzahl sind nun alle ungültigen Sperrmuster nach der Sprungregel abzuziehen, also diejenigen Kombinationen, die mindestens eine der folgenden Verbindungen enthalten: \(1\rightarrow 3, 3\rightarrow 1, 4\rightarrow 6, 6\rightarrow 4, 7\rightarrow 9, 9\rightarrow 7, 1\rightarrow 7, 7\rightarrow 1, 2\rightarrow 8, 8\rightarrow 2, 3\rightarrow 9, 9\rightarrow 3, 1\rightarrow 9, 9\rightarrow 1, 3\rightarrow 7, 7\rightarrow 3\). Hinzu addieren wir alle Kombinationen, die fälschlicherweise von der vorangegangenen Subtraktion ausgeschlossen wurden, also alle, in denen vor dem jeweiligen Übergang \(m\rightarrow n\) der Knoten \(\dfrac{m+n}{2}\) bereits ausgewählt wurde. So ist also z.B. \(5\rightarrow 9\rightarrow 1\rightarrow 2\) gültig. Die Regel der doppelten Knotenbesuche muss nicht gesondert behandelt werden, da diese bereits durch die Verwendung des Binomialkoeffizienten berücksichtigt wurde.
Ich habe zur Berechnung ein kleines Java-Programm geschrieben (siehe Simulator.txt (9 kb)).
(Alternativer Link: https://github.com/kazutokirigayakun/Mathelounge/blob/master/Simulator.java)
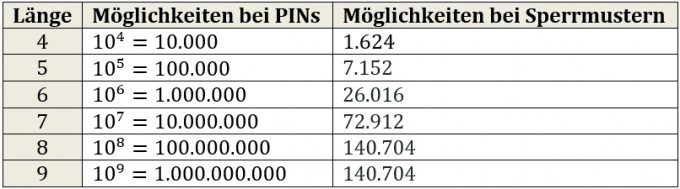
Insgesamt sind also „nur“ \(389.112\) Sperrmuster möglich, wobei die Muster der Länge \(8\) und \(9\) insgesamt ca. \(72.32\%\) ausmachen. Die Tabelle zeigt also, auf welche Vielfalt man bei der Wahl des „visuellen“ Passwortschutzes verzichtet.
Ob man nun zwecks vermeintlich simplerer Merkmöglichkeit ein Sperrmuster als Lock-Screen nutzt, muss jeder für sich selbst entscheiden.
Das Mitglied hat durch den Artikel 50 Bonuspunkte erhalten. Schreib auch du einen Artikel.