ich bin mir nicht sicher, ob ich die gemeinsame Verteilung von Zufallsvariablen richtig verstanden habe und würde mich über etwas Hilfe freuen.
Ich habe folgende Aufgabe:
3 Kinder steigen nacheinander in ein Karussel ein. Das Karussel sieht so aus:
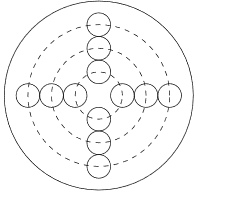
Die Kinder suchen sich dann jeweils einen unbesetzten Platz.
Nun sei Xi die Anzahl der Kinder in der i-ten Bank und Yj die Anzahl der Kinder in der j-ten Umlaufbahn.
a) Bestimme die gemeinsame Verteilung von X1,X2,X3,X4.
b) Bestimme die gemeinsame Verteilung von X1,Y2.
c) Bestimme die Verteilung der Anzahl leerer Bänke.
a)
Habe die Permutationen zusammengefasst:
P(X= {1,1,1,0} ) = 3/12 * 3/11 *3/10 * 4 *6=27/55 | 4 Permutationen , 6 Ereignisse führen jeweils zu den Permutationen
P(X = {2,1,0,0}) = 3/12 * 2/11* 3/10 *12*3 =27/55 | 12 Permutationen , jeweils 3 Ereignisse führen zu den Permuationen
P(X= {3,0,0,0}) = 3/12*2/11*1/10 = 1/55 | 4 Permutationen ,jeweils nur 1 Ereignis
Kann man das so machen?
Auf die Permutationen komme ich ja per (4 tief 1)*(1 tief 1) (bei 1 und 3) und (4 tief 2)*(2 tief 1) (bei 2)
b)
Kann ich dies also mit dem selben Ansatz wie folgt bearbeiten? Komme ich da irgendwie anders drum rum,statt anzuschauen, wie hoch die Wahrscheinlichkeit für eins der Ereignisse ist und wie oft dieses Ereignis auftritt? Ergebnisse lasse ich vorerst mal raus.
P(X1,Y2) :
P(X1 =1, Y2=1) =
P(X1 =2,Y2=1) =
P(X1 =3,Y2=1)=
P(X1= 1,Y2=2) =
P(X1= 2 ,Y2=2)=
P(X1=3 , Y2= 2)=0
P(X1= 1,Y2=3) =
P(X1= 2 ,Y2=3)= 0
P(X1=3 , Y2= 3)= 0
c)
Verstehe ich das richtig, dass dies im Endeffekt X ist , nur die Prozentwerte sind anders zugeordnet?
P(Z):
P(Z=1)= P(X= {1,1,1,0} )
P(Z=2) = P(X = {2,1,0,0})
P(Z=3) = P(X= {3,0,0,0})