Pythagoras: Zylinderförmiges, 14 cm hohes Longdrinkglas mit Knick-Strohhalm.

Question

In ein zylinderförmiges, 14 cm hohes Longdrinkglas mit einem Durchmesser von 6,8 cm wird - so schräg wie möglich - ein Knick - Strohhalm gestellt. Der Strohhalm ist 24 cm lang, die Knickstelle befindet sich 6cm vom Strohhalmende entfernt.

a) Wie weit ragt der Strohhalm ungeknickt über den Glasrand hinaus?

b) Klaus knickt den Strohhalm rechtwinklig ab. Wie weit sind nun die beiden Strohhalmenden voneinander entfernt?

Answer 1

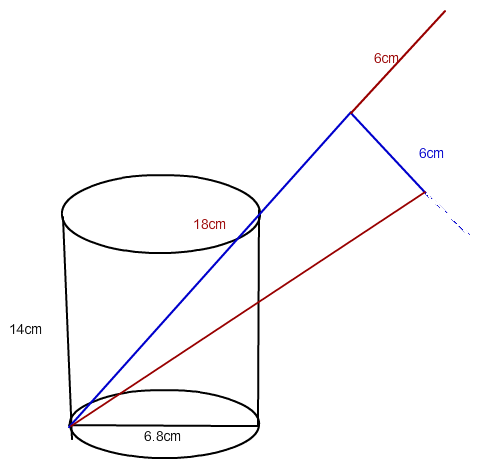
b) ist einfacher

d= √(18^2 + 6^2) = 18.93 cm

a) Diagonale des Glases

c = √(6.8^2 + 14^2) = 15.56 cm

Restlänge des Halms (aus dem Glas ragend) r = 24 - 15.56 = 8.44 cm. fertig!

Zusatz (Ich glaube nicht, dass das bei a) so gemeint ist, könnte aber so gelesen werden): Vertikal ragt der Halm h über das Glas.

h lässt sich aus folgendem Verhältnis berechnen:

h / r = 14/ c       |*r

h = 14r / c = 14*8.44 / 15.56 = 7.59 cm