Gleichung der Gesamtkostenfunktion bestimmen: Die Fixkosten sind 10 GE. Bei einer Produktionsmenge…

Question

Hi, ich habe ein hausaufgabenproblem:

Es geht darum die Gleichung der Gesamtkostenfunktion K zu bestimmen.

Die Fixkosten sind 10 GE.
Bei einer Produktionsmenge von 3 ME ist der Zuwachs der Gesamtkosten am geringsten und beträgt 3ME/GE.

Bei der Kapazitätsgrenze (8ME) betragen die Gesamtkosten 186GE.
Ich soll das ganze mit meinem Taschenrechner lösen, deshalb brauche ich einfach Werte, mit denen ich arbeiten kann.
So weit bin ich schon selbst:

K(x)= axX^3+bxX^2+cxX+d

K(0)=ax0^3+bx0^2+cx0+d=10

K(8)=ax8^3+bx8^2+cx8+d=186

und für K(3) braucht man die 2. Ableitung, da der Zuwachs am geringsten ist, was auf einen Wendepunkt hinweist, also
K"(X)= 6aX+2b

aber ab hier komme ich nicht mehr weiter v.v

Ich brauche die Hausaufgabe Mittwoch in der Schule, wäre toll, wenn ich bis da hin ein bisschen Hilfe bekomme:)

Answer 1

K(x) = ax^3 + bx^2 + cx + d
K'(x) = 3ax^2 + 2bx + c
K''(x) = 6ax + 2b

Die Fixkosten sind 10 GE.

K(0) = 10
d = 10

Bei einer Produktionsmenge von 3 ME ist der Zuwachs der Gesamtkosten am geringsten und beträgt 3ME/GE.

K''(3) = 0
18a + 2b = 0

K'(3) = 3
27a + 6b + c = 3

Bei der Kapazitätsgrenze (8ME) betragen die Gesamtkosten 186GE.

K(8) = 186
512a + 64b + 8c + d = 186

Wir haben das Lineare Gleichungssystem

d = 10
18a + 2b = 0
27a + 6b + c = 3
512a + 64b + 8c + d = 186

Die Lösung ist a = 1 ∧ b = -9 ∧ c = 30 ∧ d = 10

Die Kostenfunktion lautet daher

K(x) = x^3 - 9x^2 + 30x + 10

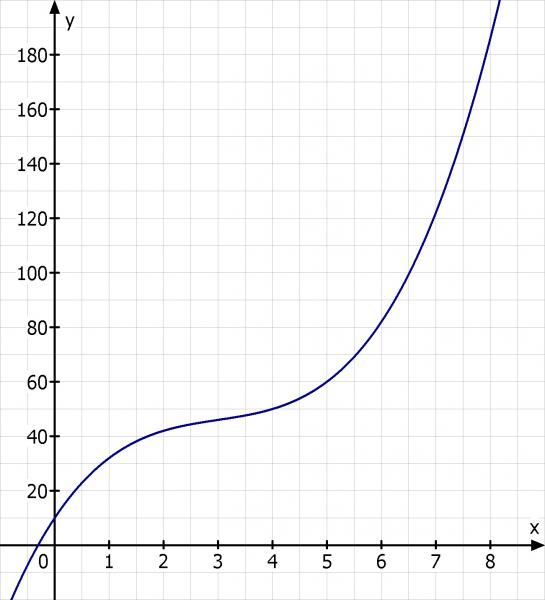
Skizze: