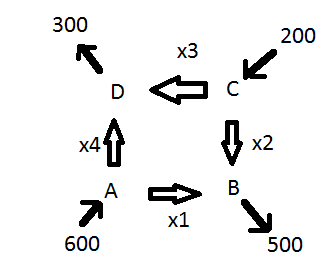
wenn man das Gleichungssystem aufstellt und zu lösen versucht, so stellt sich heraus, dass die Matrix nur den Rang 3 hat und somit nicht eindeutig zu lösen ist.
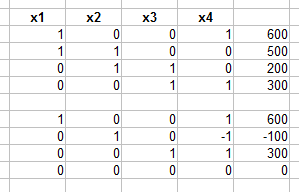
Setzt man \(x_4=t\) so lassen sich die weiteren Verkehrsdichten aus der unteren Matrix ablesen
$$x_1=600-t$$
$$x_2=t-100$$
$$x_3=300-t$$
sperrt man die Verbindung AD so müsste \(x_4\) und damit \(t\) zu 0 werden. Dann wäre aber \(x_2=-100<0\), eine negative Verkehrsdichte, was nicht möglich ist. Die Frage in a) ist also mit Nein zu beantworten.
zu b) es ist nach der minimalen Verkehrsdichte von \(x_1\) gefragt. Um \(x_1\) möglichst klein zu machen, muss \(t\) möglichst groß sein. \(t\) wird durch \(x_3=300-t\) beschränkt. Hier kann \(t\) maximal zu 300 werden. Also ist \(x_{1 \space min}=600-300=300\)
zu c) es ist nach der maximalen Verkehrsdichte von \(x_3\) gefragt. Hier muss \(t\) möglichst klein werden. Das Minimum ist \(t_{min}=100\) wegen \(x_2=t-100\). Dann ist \(x_{3 \space min}=300-100=200\).
Falls noch Fragen offen sind, so melde Dich bitte.
Gruß Werner