Aufgabe:
5 Gegeben sind Trapeze \( \mathrm{PQ}_{\mathrm{n}} \mathrm{R}_{\mathrm{n}} \mathrm{S}_{\mathrm{n}} \) mit den Grundseiten \( \left[\mathrm{PQ}_{\mathrm{n}}\right] \) und \( \left[\mathrm{R}_{\mathrm{n}} \mathrm{S}_{\mathrm{n}}\right] . \)
Die Punkte \( \mathrm{Q}_{\mathrm{n}}(\mathrm{x} | \mathrm{y}) \) liegen auf der Geraden h mit \( \mathrm{y}=1 \)
und die Punkte \( \mathrm{R}_{\mathrm{n}}(\mathrm{x} |-\mathrm{x}+11) \) auf der Geraden \( \mathrm{g} \) mit \( \mathrm{y}=-\mathrm{x}+11 . \)
Die Strecken \( \left[\mathrm{R}_{\mathrm{n}} \mathrm{S}_{\mathrm{n}}\right] \) haben stets die Länge 2 LE.
Es gilt: \( \mathrm{P}(0 | 1) \)
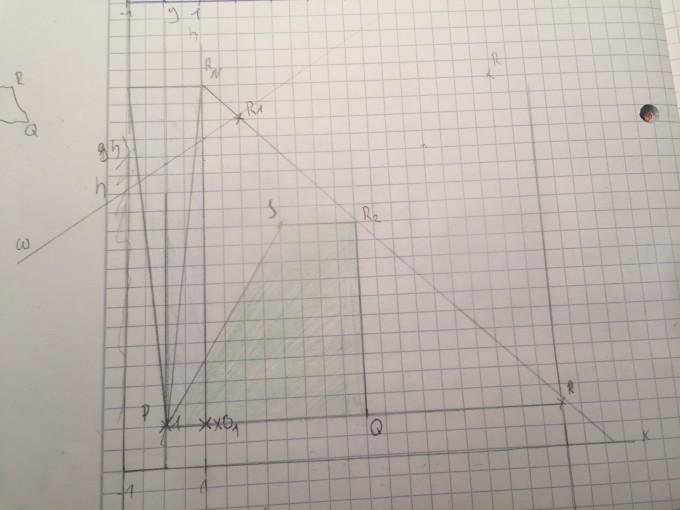
a) Zeichne zwei Trapeze \( \mathrm{PQ}_{1} \mathrm{R}_{1} \mathrm{S}_{1} \) und \( \mathrm{PQ}_{2} \mathrm{R}_{2} \mathrm{S}_{2} \) für \( \mathrm{x}=1 \) und \( \mathrm{x}=5 \).
b) Für welche Belegungen von \( x \) existieren Trapeze \( P Q_{n} R_{n} S_{n} ? \)
c) Ermittle durch Zeichnung und durch Rechnung die Belegung von x, für die der Punkt \( \mathrm{R}_{3} \) des Trapezes \( \mathrm{PQ}_{3} \mathrm{R}_{3} \mathrm{S}_{3} \) zusätzlich auf der Geraden w mit \( y=0.6 \mathrm{x}+7.8 \) liegt.
d) Berechne den Flächeninhalt der Trapeze \( P Q_{n} R_{n} S_{n} \) in Abhängigkeit von \( x \).
$$ \text { [Ergebnis: }\left.\mathrm{A}(\mathrm{x})=\left(-0,5 \mathrm{x}^{2}+4 \mathrm{x}+10\right) \mathrm{FE}\right] $$
e) Berechne den Flächeninhalt des Trapezes \( \mathrm{PQ}_{3} \mathrm{R}_{3} \mathrm{S}_{3} \)
1) Für welche Belegung von x wird der Flächeninhalt eines der Trapeze maximal?
Ich schreibe morgen eine Schulaufgabe 9.Klasse Realschule Bayern und beim üben konnte ich eine Frage nicht beantworten
Flächeninhalt im Trapez in Abhängigkeit von X berechnen
Kann mir vielleicht jemand sagen wie das klappt?
Das ist Nummer d mit Lösung