Extremalprobleme Rechteckige Konzertbühne von mindestens 400m^2 möglich?

Question

Für das Konzert von Tokio Hotel soll eine rechteckige Bühne errichtet werden. Sie soll in die abgebildete Grundstücksecke, die ein gleichschenkliges Dreieck mit der Hypotenuse von 50 m ist, eingepasst werden. Die Fläche der Bühne soll mindestens 400 m^2 betragen. Ist diese Forderung erfüllbar?

Answer 1

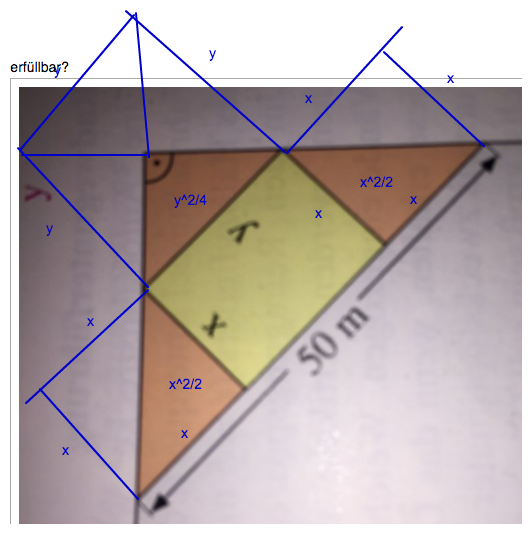
Eingezeichnet Quadrate und Strecken, von denen ich unten spreche. 

Das gleichschenklige Dreieck hat zwei Basiswinkel von je 45°. Es ist ein halbes Quadrat.

Das gilt für die auch für die 3 kleineren Dreiecke im Bild. Ihre Flächen sind zwei mal (x^2/2)  und ein mal y^2/4 .

Zusammen haben die Dreiecke eine Fläche von x^2 + y^2/4

Zielfunktion:

A(x,y) = 50^2 / 4  - x^2 - y^2/4.

Nebenbedingung: Auf der Hypotenuse des grossen Dreiecks hast du  x + y + x = 50 

Also y = 50-2x

Einsetzen in A(x,y)

A(x) = 50^2 / 4 - x^2 - (50 - 2x)^2/4 

A(x) = 25^2 - x^2 - (25-x)^2/4 

Bitte erst mal nachprüfen und dann A(x) weiter vereinfachen und danach selbst ableiten und Ableitung Null setzen. 

Answer 2

Warum beträgt die Fläche des Dreiecks

1/4 * 50 * 50 = 625 m²

Warum kann die Bühne daher maximal 312.5 m² groß sein?

Comments

Hallo Coach,

Stelle ich mir das Ganze als Dachraum
vor so ist die Höhe 25 m.
Die maximale Fläche der rechten Hälfte wäre
bei x = 12.5 und y = 12.5 ( aus Erfahrung )
12,5 * 12.5 = 156.25
Und das mal 2 = 312.5 m^2