Hallo Maurice,
dann reichen die Angaben um \(AB\) zu berechnen.
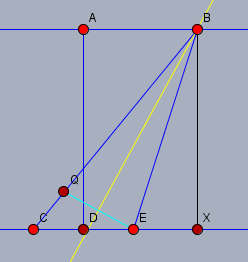
Die Strecke \(CX\) sei \(x\) und die Strecke \(QB=EB\) sei \(y\). Der Abstand \(AD\) sei \(a\) und das Delta \(CQ=0,5\text{cm}\) sei \(d\). Dann betrachte ich die rechtwinkligen Dreiecke \(CXB\) und \(EXB\).
$$x^2 + a^2=(y+ d)^2$$
$$(x-e)^2+ a^2= y^2$$
\(e\) ist die Strecke \(CE=3\text{cm}\). Sind zunächst mal zwei Gleichungen - die ziehe ich beide von einander ab
$$\Rightarrow 2xe - e^2 = 2yd + d^2 \quad \Rightarrow y=\frac{2xe - e^2 - d^2}{2d}$$
und das setzte ich in die erste Gleichung ein
$$x^2 + a^2=\left(\frac{2xe - e^2 - d^2}{2d}+ d \right)^2$$
$$x^2\left( 1 - \frac{e}{d}\right) - x\frac{e(d^2-e^2)}{d^2} + a^2 - \left( \frac{d^2-e^2}{2d}\right)^2=0$$
Ich hoffe das stimmt. Überprüfe es noch mal. Die Strecke \(AB\) ist dann \(=x-e/2\). Ich komme auf \(AB \approx 6,85\text{cm}\).
Gruß Werner