Quadratische Pyramide: Neigungswinkel einer Seitenfläche/Seitenkante, drei Innenwinkel der Seitenflächen

Question

Aufgabe:

Bei einer quadratischen Pyramide beträgt die Länge der Grundkante $a=12 \mathrm{cm}$ und die Höhe $\mathrm{h}=15 \mathrm{cm}$

a) Wie groß ist der Neigungswinkel $\alpha$ einer Seitenfläche?

b) Wie groß sind die drei Innenwinkel der Seitenflächen?

c) Wie groß ist der Neigungswinkel $\beta$ einer Seitenkante?

d) Löse die Teilauffabe a bis c für die Cheopspyramide $(a=227 \mathrm{m}, \mathrm{h}=137 \mathrm{m})$

Answer 1

a)

Neigungswinkel der Seitenfläche ist alpha hier:

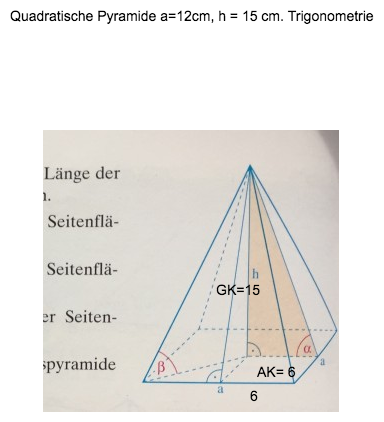
tan(alpha) = Gegenkathete / Ankathete = GK / AK = 15/6

alpha = arctan(15/6) ≈ 68.2°

c) beta

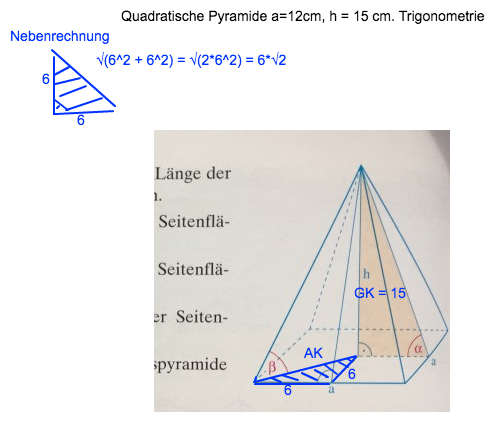
beta = arctan(GK / AK) = arctan(15/(6*√2)) ≈ 60.5°

Bei b) suchst du die Winkel gamma und delta in:

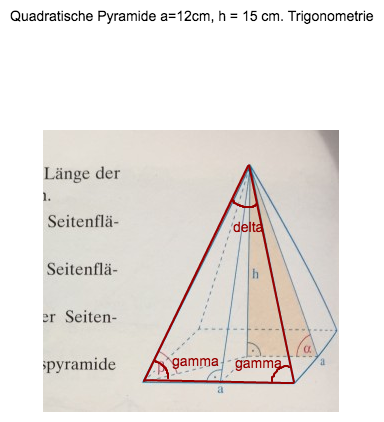
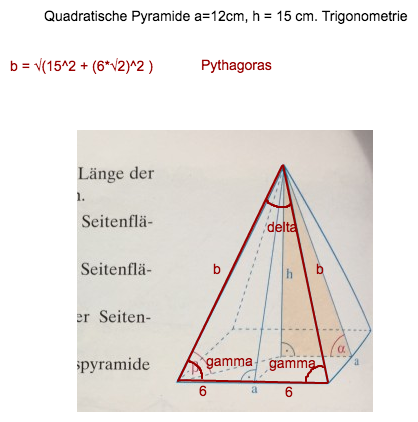
b = √(225 + 72) =  √(297)

gamma hat AK 6 und HYP √(297)

gamma = arccos( 6 / √(297) ) ≈ 69.63°

delta = 180° - 2*gamma ≈ 40.74°

Bei d) machst du dasselbe nochmals mit andern Zahlen. Das kannst du ja nun selbst.

Zur Kontrolle von d_(a) und d_(c) https://www.matheretter.de/rechner/pyramide