219 rote Halbkreise. Gleichung mit einer Variable möglich?

Question

Hallo 

Ich brauche bei folgender Aufgabe Hilfe. Mein Bruder ist in der 8. Klasse und kennt Gleichungen nur mit einer Unbekannten.

Ich kann dies aber nur mit zwei Unbekannten lösen. Gibt es einen anderen Weg, der mich nicht einfällt? Oder kann man dies nur mit einem Gleichungssystem aus 2 Variablen lösen?

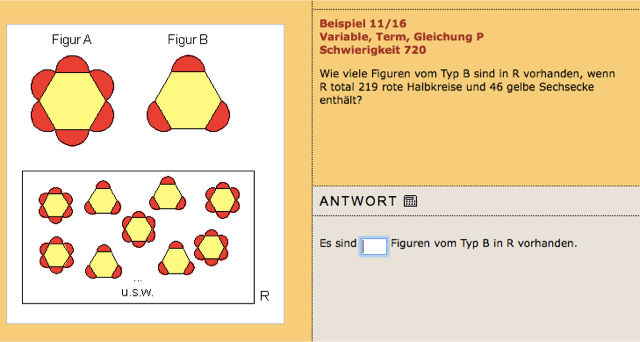
Anzahl Figuren A: x

Anzahl Figuren B: y

x + y = 46
6x + 3y = 219

x= 46 - y

6(46 - y)  + 3y = 219 

....

-> Resultat nach Auflösung: x = 27 und y = 19 -> Probe: 27 * 6 + 19 * 3 = 219 -> 162 + 57 = 219 -> Richtig

für die Hilfe!

Comments

Du kannst von Anfang an die zweite gesuchte Zahl mit Hilfe der x darstellen.

Anzahl Figuren A: x

Anzahl Figuren B: 46-x

und dann direkt: 

6x + 3(46-x) = 219

usw. 

Answer 1

Hallo MrSiv,

Willkommen in der Mathelounge.

Man kann die Aufgabe - sagen wir mal - mehr anschaulich lösen: Zu jedem Sechseck gehören entweder 3 oder 6 Halbkreise - aber eben mindestens 3. D.h. auf 46 Sechsecke kommen mindestens 3*46=138 Halbkreise. Dann verbleiben 219-138=81 Halbkreise, die es ausschließlich bei den Figuren vom Typ A unterzubringen gilt. Das sind jeweils 3 zusätzliche Halbkreise pro Figur, also müssen genau 81/3=27 Figuren vom Typ A vorhanden sein. Da pro Figur in jedem Fall nur ein Sechseck benötigt wird, bleiben 46-27=19 Figuren vom Typ B über.

Answer 2

1.) Wer es kann kann direkt schreiben
Anzahl Figuren insgesamt : 46
y : Anzahl Figuren B
6 * ( 46 - y )  + 3 * y = 219
y = 19

2.) Besser ist es aber die beiden Aussagen zunächst
getrennt in 2 Gleichungen mit 2 Unbekannten
hinzuschreiben und dann durch Einsetzung oder
andere Verfahren das sogenannte " lineare
Gleichungsssytem " zu lösen.

Später wirst du noch lineare Gleichungssysteme
mit 3 oder mehr Unbekannten ( 3 Gleichungen
vonnöten ) lösen müssen.
Da ist die Vorgehensweise 2.) angesagt.

mfg Georg