Behauptung: Funktionenschar fk (x) = - (x-k)^2 + k hat eine gemeinsame Tangente

Question

f_k (x)   =    - (x-k)^2  + k

 

Es gibt eine gemeinsame Tangente für die Graphen aller Funktionen k ∈ R  .

 

Dank für eure Hilfe

Comments

Hast du versucht eine gemeinsame Tangente für 

y   =    - (x-k)²  + k    und y = -(x-m)^2 + m

zu finden?

Oder für 

y  =    - (x)²     und y = -(x-1)^2 + 1 ?

Wenn es hier nur eine gäbe, hättest du wohl bereits die gesuchte gemeinsame Tangente für alle Kurven.

---

Ich habe mich gefragt an welchen Punkten die gleich Steigung vorliegt ....

f´(x) =  -2x +2k      -> keine lsg


aber danke ich versuch es mal so

---

keine chance ich bekomm es nicht raus :(

Answer 1

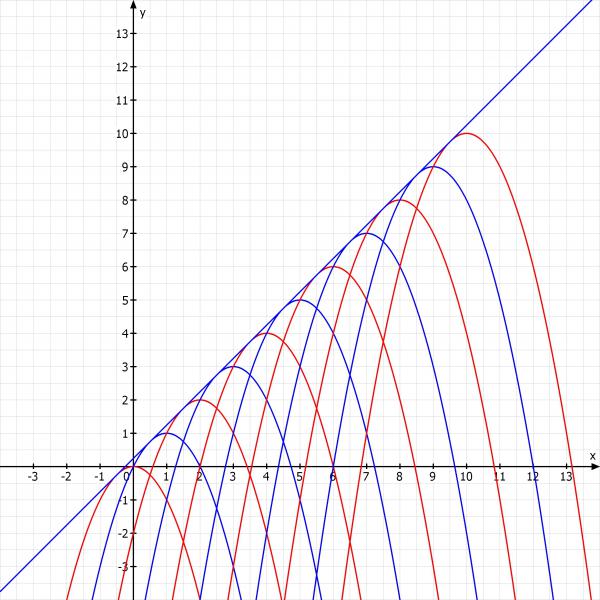
Das handelt sich ja um nach unten geöffnete Normalparabeln, deren Scheitelpunkt bei (k, k) also auf einer Ursprungsgeraden liegen. Daher sollte die Gemeinsame Tangente auch die Steigung 1 haben.

Also schau ich wo wir die Steigung 1 haben

f₀(x) = -x^2

f₀'(x) = -2x = 1
x = -1/2

t(x) = 1(x + 1/2) + f₀(-1/2) = x + 1/2 - 1/4 = x + 1/4

Skizze

Comments

Danke ..... also muss man sich erst den Verlauf der Funktion anschauen . Also ohne den kann man nix machen ?

---

Ja. So würde ich das zumindest machen weil das wohl am einfachsten ist. Allerdings ist der Verlauf hier ja auch recht einfach abzulesen gewesen.

Answer 2

Ich hab eine rechnerische Lösung. Graphisch klappt das bei mir jetzt auch.

https://de.wikipedia.org/wiki/Tangente

y = f(xo) + f'(xo)(x-xo)

to an der Stelle xo an y = -x^2

y' = -2x

to: y = -xo^2 - 2xo(x-xo)

            = -xo^2 - 2xo*x+2xo^2  -2xo*x + xo^2

t1 an der Stelle x1 an y = -(x-1)^2 + 1 = x^2 " 2x

y' = - 2x + 2

t1: y = -x1^2 + 2x1 + (-2x1+2)(x-x1)

= (-2x1 + 2)x - x1^2 + 2x1 + 2x1^2 - 2x1

=(-2x1 + 2)x + x1^2

Steigung gleich:

-2xo = - 2x1 + 2       |:-2

xo = x1 - 1

y-Achsenabschnitt gleich

xo^2 = x1^2

Einsetzen

(x1-1)^2 = x1^2

x1^2 - 2x1 + 1 = x1^2

-2x1 + 1 =0
x1 = 1/2 → t1: y = x + 1/4

xo = - 1/2    -------> t2: y = x+1/4

Und jetzt einfach noch prüfen, ob diese Gerade alle Parabeln der Schar genau in einem Punkt schneidet.