Bestimmung von Stammfunktionen von 1. f (x)= 3/x^2

Question

Undzwar gibt es folgen Aufgaben , die ich beim besten Willen nicht integrieren kann.

1. f (x)= 3/x^2 

2. f (x)= x^2/2 + 4/x^3

3. f (x)= n^2x^n-1

Vorab , danke für jede Hilfe .

Gruß xtream_26

Comments

Wie sieht 3. genau aus? 

---

Hab mich bei der 3 vertippt, sorry :)

Die eigentliche Aufgabe lautet :

f (x)= n^2x^n-1

---

??? Mach vielleicht einen Abstand, wenn der Exponent zuende ist. Klammern um den Exponenten sollten das Problem beheben. 

Answer 1

Verwende Potenzen mit negativen Exponenten. 

Dann genügt, falls n≠0 und n≠ -1: 

f(x) = x^n  

F(x) = 1/(n+1) x^{n+1} + C 

1. f (x)= 3/x² = 3x^{-2} 

F(x) = 3*1/(-1)*x^{-1} + C

= -3/x  + C 

2. f (x)= x²/2 + 4/x³ = 0.5 x^2 + 4 x^{-3} 

F(x) = 0.5 * 1/3 * x^3 + 4*1/(-2)*x^{-2} + C 

= 1/6 x^3 - 2/x^2 + C

ohne Gewähr.

Kontrolle mit https://www.wolframalpha.com/input/?i=x%5E2%2F2+%2B+4%2Fx%5E3

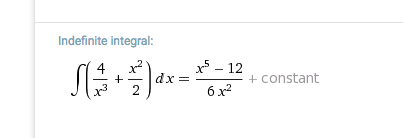
Mein Resultat bei 2. scheint zu stimmen. 

Comments

Alles klar , vielen Dank für deine Bemühungen.  

Gruß