Wie sieht diese Ungleichung aus: y > -| x-4 | -3

Question

Eine ungefähre Zeichnung reicht. Ich weiß nicht was das Minus in den Betragsstrichen bewirkt.

Comments

Zur Kontrolle kannst du dir deine Ungleichungen auch hier aufzeichnen lassen. Einfach anpassen.

https://www.wolframalpha.com/input/?i=y%3E+-+abs%28x-4%29+-3+

Answer 1

Hi clara,

man kann hier wieder das Extremum suchen, indem man dafür sorgt, dass der Betrag 0 wird.

y>-|x-4|-3

-> y=-|4-4|-3=-3

 

Also für x=4 und y=-3 hat man sein Maximum gefunden.

Nun sieht man ja außerdem, dass wir nur die Steigung x haben. Also eine Gerade welche den Winkel 45° hat, bzw. eine parallele zur Winkelhalbierenden. Wegen dem Betrag hat diese beim Maximum einen Knick. Letztlich solltest Du so etwas auf Papier bringen:

 

 

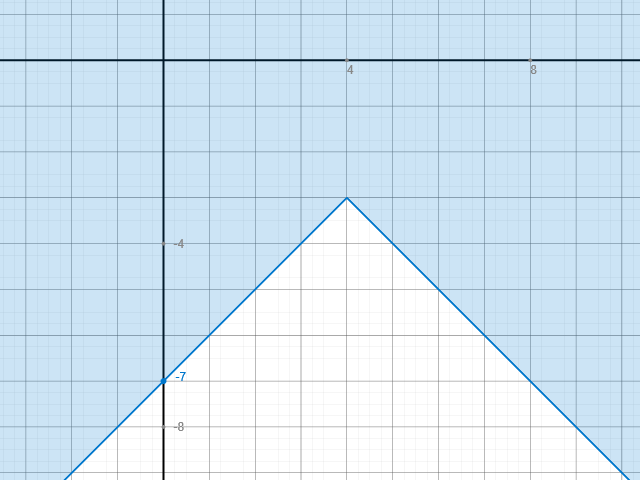
Solltest Du es nicht sehen können. Also die Steigung des Graphen, kannst Du Dir auch schnell eine Wertetabelle machen. Setze x=2,3,4,5,6 ein und das sollte schon ausrechen. Welche Fläche Du dann schraffieren musst -> Nun wir wollen ja y größer haben, also ist es jene Fläche über der "Pyramide".

 

Grüße

Answer 2

|x - 4| kann minimal den Wert 0 annehmen (das ist ja bei Ausdrücken in Betragsstrichen immer der Fall), und zwar für x = 4; sonst ist |x - 4| immer größer als 0.

Wenn wir also den minimalen Wert einsetzen, erhalten wir:

y = - |4 - 4| -3 = -3

Nehmen wir jetzt für x zum Beispiel den Wert -10, dann erhalten wir:

y = - |-10 - 4| - 3 = -14 - 3 = -17

Und jetzt noch für x den Wert +10:

y = - |10 -4| - 3 = -6 - 3 = -9

Wenn ich mich zu so später Stunde nicht verrechnet habe (bitte nachprüfen!), dann haben wir wieder einen umgekehrt V-förmigen Graphen mit einem globalen Maximum an (4|-3)