Verpackung Schokoladenbonbons Pyramidenstumpf: Bestätige dass Punkt Fh auf der Kante liegt

Question

Aufgabe:

Eine Firma plant eine neue Verpackungsform für Schokoladenbonbons. Bisher wurde das Produkt in einer Verpackung der Form eines regelmäßigen Pyramidenstumpfes verkauft. Die Punkte $A(10|0|0), B(10|10| 0)$ $\mathrm{C}(0|10|0), \mathrm{D}(0|0|0)$ und $\mathrm{G}(8|2|8)$ beschreiben einige Eckpunkte ( $1 \mathrm{LE}$ entspricht $1 \mathrm{cm}$ ).

Im Jubiläumsjahr der Firma soll die Form leicht variliert werden. Dazu soll die Schachtel entlang einer Ebene durch die Punkte $E, S_{1}$ und $S_{2}$ geteilt werden, sodass eine neue Deckfläche entsteht. Die Punkte $S_{1}(9|1| 4)$ und $S_{2}(1|9| 4)$ sollen dabei fest sein und $E_{h}(h|h| 4 h)$ mit h ∈ ℝ wird entlang der hinteren Kante $k_1$ variert.

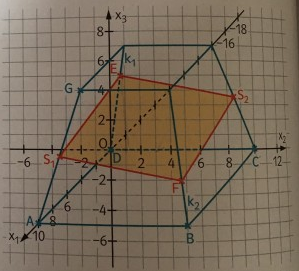
a) Geben Sie den Definitionsbereich für h an, sodass die Punkte $E_h$ auf der hinteren Kante $k_1$, des Pyramidenstumpfes liegen.

b) Bestätigen Sie, dass die Punkte $F_{h}$ auf der vorderen rechten Kante $k_{2}$ des Pyramidenstumples durch $F_{h}\left(\frac{7 h-25}{h-3}\left|\frac{7 h-25}{h-3}\right| \frac{12 h-20}{h-3}\right)$ beschrieben werden.

c) Untersuchen Sie, welche Form die Deckfläche für $h=1$ hat.

d) Um für die neue Form der Verpackung den Pyramidenstumpf beizubehalten, soll der Punkt $f_h$ auf der Kante $\mathrm{k}_{2}$ liegen. Ermitteln Sie die Werte für h, für die diese Bedingung erfüllt ist. Interpetieren Sie Ihr Ergebnis im Sachzusammenhang.

Ansatz/Problem:

Ich habe Schwierigkeiten gehabt zu zeigen, dass der Punkt Fh auf der vorderen Kante k2 liegt. Hier meine Lösung. Ist das richtig?

 

Vielen Dank für die Hilfe :)

Comments

Verweis: https://www.mathelounge.de/671964/punkte-auf-kante-eines-pyramidenst…

Answer 1

Ich habe Schwierigkeiten gehabt zu zeigen, dass der Punkt Fh auf der vorderen Kante k2 liegt.

Das ist nicht die Aufgabenstellung. Der Punkt F_h liegt bereits laut Voraussetzung auf der Kante k₂. Aufgabe ist, zu zeigen dass er die in b) angegebenen  Koordinaten hat.

Du sagst, es müss P ermittelt werden. In der Zeichnung und im Text gibt es kein P. Wenn du neue Bezeichnungen einführst, dann solltest du erwähnen, wofür sie stehen.

Wenn P das ist, was ich glaube (der andere Endpunkt der Kante k₂), dann ist $\vec{AG} = \vec{BP}$ falsch. Es handelt sich um einen Pyramidenstumpf, da sind die Kanten nicht parallel.

Stattdessen: Sei M(m₁ | m₂ | 0) der Mittelpunkt der Grundfläche. Zieht man eine Gerade durch A und G, dann verläuft sie durch einen Punkt Z(m₁ | m₂ | x₃). Berechne Z. Die Gerade von der k₂ ein Teil ist, verläuft ebenfalls durch Z, weil sich die Seitenkanten einer Pyramide in einem Schnittpunkt treffen.

Comments

Hallo oswald,

Müsste der Definitionsbereich bei Teilaufgabe a) nicht 0<=h<=2 lauten?

Gruß