Pyramidenstumpf Vektoren

Question

Aufgabe:

Von dem abgebildeten Pyramidenstumpf sind die Punkte
A(6|0|0), B(6|6|0), C(0|6|0), E(4|2|5) und F(4|4|5) gegeben.
Die Deckfläche EFGH ist ein Quadrat.
P und Q sind die Mittelpunkte der Seiten BC und FG.

a) Ermitteln Sie die Koordinaten der Punkte G und H.
Zeichnen Sie das Schrägbild des Pyramidenstumpfes in ein Koordinatensystem.

b) Untersuchen Sie die gegenseitige Lage der drei Geraden AQ, BH
und EP zueinander.

c) Ergänzen Sie den Pyramidenstumpf zu einer Pyramide. Bestimmen Sie die Koordinaten der Pyramidenspitze
S.

Problem/Ansatz:

Hallo,

ich komme mit dieser Aufgabe leider nicht so richtig zurecht.

Fangen wir am besten zunächst mit a) an. Hier habe ich alles rausgefunden und optimal bearbeitet.

Nun scheitert es aber bei B) und C), trotz Lösungsansätze und Tipps verstehe ich die beiden Aufgaben nicht so recht...

Könnte die eventuell einer mit Lösungsweg erklären?

MfG

Comments

Vom Duplikat:

Titel: Pyramidenstumpf. Lagebeziehungen zwischen Geraden?

Stichworte: lagebeziehung,geraden,vektoren,pyramidenstumpf,analytische-geometrie

das ist meine Aufgabe (18).

Ich habe folgende Punkte herausgefunden:

D(0|0|0)    G(0|4|5)    H(0|2|5)    P(2|6|0) und Q(2|4|5). Ist das richtig?

Ich weiß jetzt nicht wirklich, was ich bei b) machen muss. Soll ich erstmal die Gerade von AC, BH und EP berechnen ?

Gruß.

---

Das Bild zur Aufgabe:

(klick auf das Bild)

Answer 1

Da ist was falsch  G(0|4|5)    H(0|2|5) 

denn dann wäre es von E nach H ja die Länge 4,

aber von E nach F ist es nur 2.

Deshalb ist wohl      G(2|4|5)    H(2|2|5)  richtig.

Und dann stellst du die Geradengleichungen auf und setzt sie

jeweils gleich.

Dann bekommst du die gegenseitige Lage heraus.

c) Für die Spitze schneidest du einfach AE mit BF die treffen

sich ja in der Spitze.

Comments

Ohh ok, dankeschön. Dass heißt das Q dann (1|3|4) ist richtig?

Danke für die Ansätze für b) und c).

Answer 2

B)

Kannst du bei B) zunächst die Punkte P und Q berechnen?

Kannst du dann die 3 Geraden (g, h, i) aufstellen?

Die Lage zweier Geraden kann sein: identisch, parallel, schneidend oder windschief.

Kannst du jetzt die Lage der 3 Geraden zueinander bestimmen. Also g zu h, g zu i und h zu i.

C)

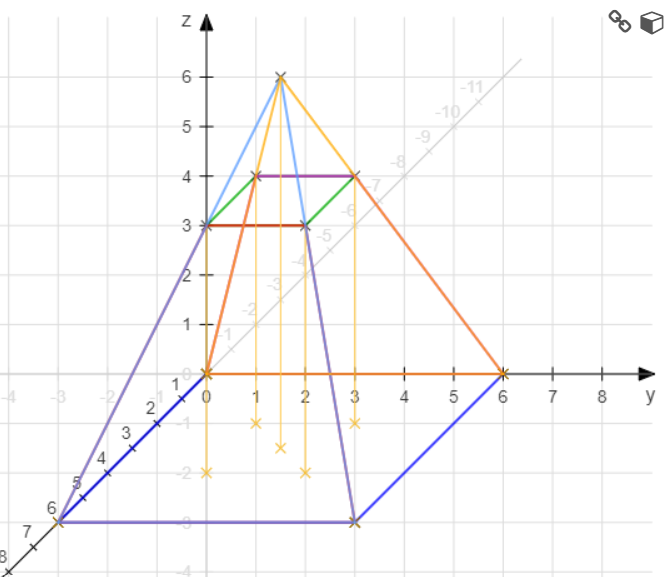
Hier könntest du zunächst die Pyramidenspitze S bestimmen. Du könntest am einfachsten den Strahlensatz nehmen um die Höhe zu bestimmen. h/6 = (h - 5)/2 --> h = 7.5

Die x und y-Koordinate sollte hoffentlich klar sein oder?

Jetzt den Pyramidenstumpf ergänzen geht auch oder?

Hier noch zur Hilfe eine Skizze der Pyramide

Comments

Ich wüsste nicht, wie man eine Gerade aufstellt.

Danach aber gleichsetzen, gucken ob die Gerade ein Vielfaches ist, ein Gleichungssystem bilden...?

---

Eine Gerade durch die Punkte A und B hat die Form

g: X = A + r * AB

A ist dabei der Ortsvektor von A

AB ist der Richtungsvektor von A nach B

Dazu gibt es auch hilfreiche Videos bei Youtube.