Berechne erst mal die Gleichung für p1.
Dazu Ansatz
y = x2 + bx + c
A und B einsetzen.
A (2I5) und B (6I-3).
5 = 4 + 2b + c
-3 = 36 + 6b + c
Nun b und c ausrechnen. Dasselbe Verfahren wie bei deiner 2. Aufgabe.
Dann bringst du die Parabelgleichung am besten auf Scheitelpunktform und machst mal eine Skizze.
p: y = x^2 -10x + 21 und S(5|-4)
Nun zur Geradengleichung:
A (2I5) und B (6I-3).
Steigung m = (-3 - 5) / (6 - 2) = -8 / 4 = -2
Ansatz
g2: y = -2x + q
S einsetzen
-4 = -10 + q
6 = q
y = -2x + 6
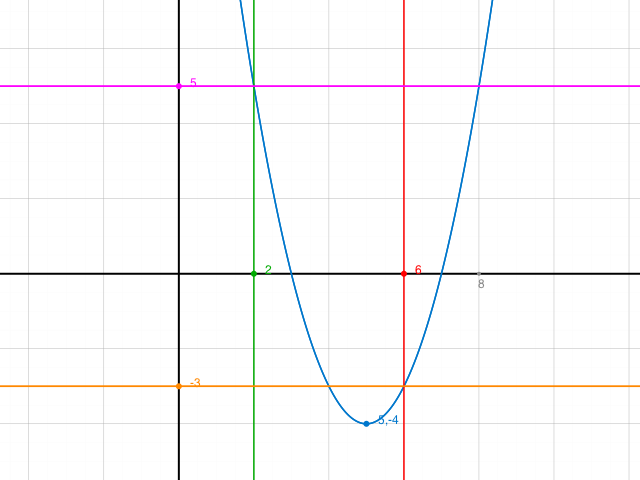
Kontrolle Graph: