Winkel zwischen Vektor a und Koordinatenachsen, habe ich richtig gerechnet? Wie komme ich auf den zweiten Winkel?

Question

-Beachte, ich arbeite hier mit Fotos weil das Einfügen des Codes nicht funktioniert-

Aufgabe
Welchen Winkel bildet Vektor a mit den Koordinatenachsen?

Lösung: 36.87°, 126.87°

Problem: Habe ich richtig gerechnet, was haltet ihr vom Rechenweg? Und wie komme ich auf den zweiten Winkel 126.87° denn ich kann kein rechtwinkliges Dreieck mit der Y-Achse bilden um dann den Winkel phi ausrechnen?




Rechenweg:


1. Was habe ich für einen Vektor?

\( \vec{a}=\left(\begin{array}{c}{4} \\ {-3}\end{array}\right) \) 
Koordinaten müssten demnach so aussehen Punkt A ( 4 I -3 )

2. Welche Steigung hat der Vektor?
m_a= -3/4

3. Die x-Achse
Wenn ich vom Endpunkt mines Vektors in Richtung  X-Achse einen weiteren Vektor ziehe ist x nichts anderes als v1.

Dann habe ich einen Winkel im rechtwinkligen Dreieck und kann das anwenden

\( \vec{a} * \vec{v}_{1}=\left(\begin{array}{c}{4} \\ {-3}\end{array}\right) *\left(\begin{array}{c}{4} \\ {0}\end{array}\right)=16+0=16 \)
\( \cos \varphi=\frac{\vec{a} * \vec{v1} }{\sqrt{\left(a_{x}\right)^{2}+\left(a_{y}\right)^{2}} * \sqrt{\left(v 1_{x}\right)^{2}+\left(v 1_{y}\right)^{2}}}=\frac{16}{20}=0.8 \)
\( \cos \varphi=0.8 / \cos ^{-1} \)
\( \varphi=36.87^{\circ} \) 

Answer 1

Hallo Limonade,

zunächst eine Skizze:

Der Tangens vom gelben Winkel \(\varphi_x\) (Winkel \(\vec{a}\) zu X-Achse) ist Gegenkathete zu Ankathete - also

$$\tan \varphi_x = \frac{-3}{4} \quad \Rightarrow \varphi = \arctan\frac{-3}{4} \approx -36,87°$$

-3 weil man in Richtung des Referenzvektors (der X-Achse) nach rechts gehen muss; und links wäre positiv.

Beim blauen Winkel (Winkel \(\vec{a}\) zu Y-Achse) ist es etwas schwieriger. Stelle Dich dazu in den Ursprung und schaue in Richtung des Referenz-Vektors - also der Y-Achse. Links wäre positiv und rechts negativ. Also musst Du für die 'Gegenkathete' -4 nach rechts. Vorne ist positiv und hinten wäre negativ, was die 'Ankathete' angeht. In diesem Fall also -3 - weil nach hinten. Es wäre demnach

$$\tan \varphi_y=\frac{-4}{-3}$$

Nun ist aber \(\frac{-4}{-3}\) dasselbe wie \(\frac{4}{3}\) - als ob der Vektor \(\vec{a}\) links neben der Y-Achse liegt (die rote Linie). Da man aber weiß, dass der Vektor 'nach hinten' zeigt, musst Du 180° abziehen (oder auch addieren, was das selbe ist! Der Winkel liegt auf der 'anderen' Seite). Also ist

$$\varphi_y= \arctan \frac{-4}{-3} - 180°= 53,13° - 180°=-126,87°$$

Falls etwas unklar ist, so frage bitte nach.

Gruß Werner

Comments

.. zu der Sache mit 'Vektor zeigt nach hinten' habe ich Dir noch mal ein Bild aus Wikipedia von der Tangensfunktion hier hinein kopiert und zusätzlich die Strecke \(\tan=4/3\) (die schwarze Strecke) hinein gezeichnet.

Du siehst, dass diese Strecke die Tangensfunktion im Intervall \((-\pi; -\pi]\) zweimal schneidet - also nimmt die Tangensfunktion zweimal den Wert \(4/3\) an. Die Umkehrfunktion ist demnach nicht eindeutig und benötigt eine zusätzliche Information um den 'richtigen' Winkel zu bestimmen.

Der Abstand zwischen zwei solcher Werte ist immer genau \(\pi\) bzw. \(180°\) - daher die \(-180°\) (s.o.)

Gruß Werner

---

@limonade

Den zweiten Winkel 126,87° zwischen \(\vec{a}\) und der y-Achse erhältst du, wenn du in deiner Formel [4,0] durch den Richtungsvektor  [0,1] der y-Achse ersetzt.

Gruß Wolfgang

---

Erster Winkel kapiert.

Super, die erste Rechnung habe ich kapiert.

 tanφ_x = -3/4  /tan^-1
φ_x = -36.87° = 36.87°

Zweiter Winkel

Wenn ich mich in den Ursprungstelle und richtung Referenzvektor (Y-Achse) schaue, 
sehe ich zunächst mal nur eine Gerade. 

Links (2. Quadrant) wäre bei mir negativ. da ich mich um vier einheiten nach links bewege.
Rechts (1. Quadrant) wäre dann bei mir gemäss Skalierung der Achsen positiv.

Deswegen ist auch der Rest für mich schwierig zu verstehen.

Wenn man den Roten Vektor diener Zeichnung zieht, hätte ich gesagt,

v_rot = ( -4 I 3 ) 

Ab hier verstehe ich es nicht mehr...

Ich kann es nur so rechnen
 ich kann es wirklich nur so lösen indem ich sage ok, anhand der Grafik sehe ich, dass der erste Quadrant noch fehlt um den Winkel mit der Y-Achse zu bekommen. 

Der erste Quadrant ist 90°

φ_x + 90° = 126.87°

---

Hallo Limonade,

Du schreibst: "Wenn ich mich in den Ursprungstelle und richtung Referenzvektor (Y-Achse) schaue,  sehe ich zunächst mal nur eine Gerade.  Links (2. Quadrant) wäre bei mir negativ."

es kommt weniger darauf an, was Du vom Ursprung aus siehst, sondern wo links (positiv drehend) oder rechts ist (negativ drehend). Mit positiv ist keine Richtung der X- oder Y-Achse gemeint, sondern die Drehrichtung, die vereinbarungsgemäß in der Mathematik nach links - also gegen den Uhrzeigersinn - positiv ist.

Rein qualitativ siehst Du, dass der Vektor \(\vec{a}\) aus der Sicht der Y-Achse sich hinten rechts - also relativ zur Y-Achse im 3.Quadranten befindet. Damit muss dieser Winkel im Intervall von \((-90°;-180°)\) liegen.

Der blaue Vektor sei hier die Y-Achse.

Aus der Sicht der X-Achse befindet sich \(\vec{a}\) im 4.Quadranten - also im Intervall \((-90°;0°)\). Kippe dazu das Bild oben 90° nach rechts.

Gruß Werner

---

Vielen, vielen Dank Werner ! Es macht bei mir nicht klick, ich muss vielleicht noch etwas üben. 

Aber ich schätze deine Hilfe sehr !

---

Hallo Limonade, ich melde mich heute abend noch mal ...

---

ich habe da mal was vorbereitet:

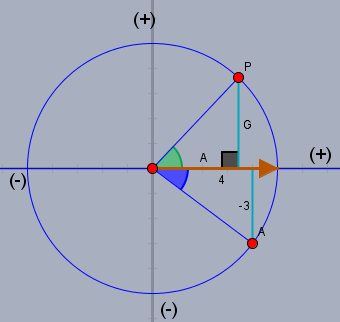
Das erste Ziel ist es, den Tangens des blauen Winkels gegenüber der Referenz (brauner Pfeil) zu bestimmen. Das kannst Du schon - nur als Wiederholung und Einstieg für das was noch kommt.

Der Tangens des grünen Winkels ist Gegenkathete zu Ankathete \(=G/A\). Die Strecken \(G\) und \(A\) haben beide Werte von größer 0 und alles ist wie Du es kennst. Wenn nun der Punkt \(P\) auf dem Kreis im Uhrzeigersinn nach unten Richtung Punkt \(A\) rutscht, dann wird die Gegenkathete \(G\) immer kleiner, schließlich zu 0 und anschließend kleiner als 0. Damit wird auch das Verhältnis \(G/A\) und damit der Tangens des blauen Winkels kleiner 0. Ist \(G=-3\) und \(A=4\) so sagt Dein Taschenrechner, das bei \(\tan \varphi_x=-3/4\) der Wert \( \varphi_x\approx -36,87°\) ist.

Wir lassen den Punkt jetzt weiter im Uhrzeigersinn laufen ...

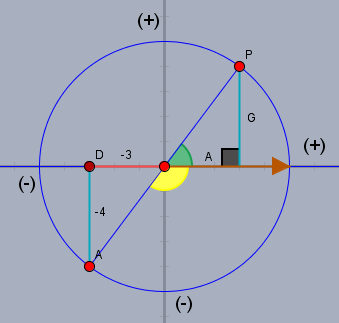
... solange bis er links unten im Bild angekommen ist. Inzwischen ist auch die Ankathete immer kleiner geworden, wurde zwischendurch zu 0 und ist nun auch negativ - und hat jetzt z.B. den Wert -3. Die Gegenkathete hat sich auch verändert, blieb aber immer negativ und soll jetzt den Wert -4 haben. Im Bild habe ich auch die Vorzeichen aus Sicht der Referenz (brauner Pfeil) eingezeichnet. Vorne und links ist positiv, hinten und rechts ist negativ. Genau wie in einem Koordinatensystem wenn die X-Achse die Referenz ist.

Der Tangens des gelben Winkels ist jetzt \((-4/-3)\) - also wieder positiv. Der Taschenrechner sagt \(53,13°\), aber der Taschenrechner rechnet den Winkel nach dem Arcustangens immer zwischen \(-90°\) und \(+90°\). Wir wissen aber, dass der Winkel im Bereich von \(-90°\) bis \(-180°\) liegen muss und das jeder Winkel mit

$$\tan{\left( 53,13° + k\cdot 180° \right)} = \frac{4}{3} \quad k \in \mathbb{Z}$$

Also mit \(k=-1\) wäre der Winkel \(53,13° - 1\cdot 180°= -126,87°\) genauso richtig.

Dritter und letzter Akt - ich drehe das ganze Bild mit allem was drin ist um 90° nach links:

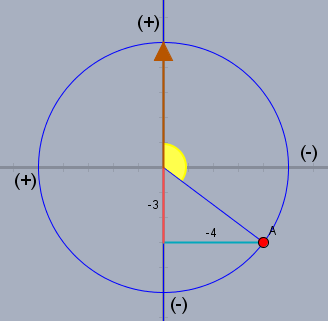
Die Referenz (brauner Pfeil) zeigt jetzt nach oben und alle Richtungen beziehen sich auf diese Referenz. Vorne (jetzt oben) und links vom braunen Pfeil ist positiv und hinten (jetzt unten) und rechst vom Pfeil ist negativ. Es bleibt also dabei
$$ \varphi_y=\arctan{\frac{-4}{-3}} \approx 53,13° + k\cdot 180°$$
Der Cosinus des gelben Winkels ist übrigens negativ, da die Hypotenuse \((=+5)\) immer positiv gerechnet wird
$$ \cos{\frac{-3}{5}} = \varphi_y \quad \Rightarrow \varphi_y=\arccos{\frac{-3}{5}}\approx\pm 126,87°$$
auch hier gibt es zwei mögliche Winkel, die diese Bedingung erfüllen, aber nur einen Winkel, der beide Bedingungen für Tangens und Cosinus erfüllt und das sind \(-126,87°\)!
Gruß Werner

---

φSuper, vielen Dank, ich hab jetzt nachvollziehen können, was du gemacht hast. Aber selber wäre ich nicht darauf gekommen, das so zu konstruieren.

Die Frage ist, in meinem buch steht wenn das Skalarprodukt gebildet werden soll dass man das produkt vom Vektor a und vektor b bildet mal den cos(phi)

Und den Winkel zwischen zwei Vektoren bekomme ich wenn ich

cosφ = a*b/a*b

Aber, ich soll glaube ich weitere Dreiecke konstruieren und mit deren Hilfe dann im rechten Galbkreis den fehlenden Winkel, der der eben nicht gezählt wird, herausfinden.

Der hätte dann

Cos(x) = -4/-3 / arcos

x = 53.13

Der gesamte Rechte Halbkreis ist 180 grad

180-53.13 = 126.17

Also komm ich auf den zweiten Winkel indem ich über die Formel hinausschaue und weitere Dreiecke und deren Winkel einzeichne und diese dann vom ganzen abziehe.

Answer 2

Hallo limonade,

deine Rechnung und das Ergebnis sind richtig.

Statt  [4, 0]  kannst du [1, 0] nehmen und bei der  anderen Achse [0, 1].

Gruß Wolfgang

Comments

Ok, ich frage wegen den Rechenwegen weil ich den Anschluss etwas verpasst habe und ich einwenig hintendrin bin. 

Und nun aus den Definitionen (Rechenoperationen mit Vektoren)  des Formelbuches die Vorgehensweise abzuleiten versuche. 

Und so nicht weiss ob die Schreibweise korrekt ist oder der Rechenweg.

Ich verstehe nicht wieso ich aus dem Vektor der vier einheitn nach rechts geht und 0 in Richtung Y-Achse auch als v1 = (1 I 0) schreiben kann ?

---

Zur oberen Rechnung sehe ich dass ich auf den zweiten Winkel komme, indem ich einfach den 1. Quadranten hinzu addiere, aber eben, ich weiss nicht ob ich anderst rechnerisch vorgehen muss

---

[1 , 0]  hat genau wie [4, 0]  die Richtung der x-Achse, so dass sich der gleiche Winkel ergibt. 

Den zweiten Winkel 126,87° erhältst du also, wenn du in deiner Formel [4,0] durch [0,1] ersetzt.

---

Hat geklappt, aber wieso darf ich den Vektor der Y-Achse (v₂) so umschreiben?

wenn ich sage dass der Vektor die Komponenten 0 und 1 hat, bedeutet das, dass er 0 Einheiten in Richtung X-Achse geht, und eine Einheit nach oben. So muss  v₂ die Koordinaten ( 0 I 1 ) haben. 

---

cos(x) = -3/5 spuckt tatsächlich den richtigen Wert (x = 126.87°) aus.

Mit diesen Angaben müsste in der Zeichnung ein Rechtwinkliges Dreieck mit folgenden Verhältnissen möglich sein. Oder? 

Ankathete / Hypotenuse = -3 / 5

Aber der Winkel zwischen Vektor a und v2 lässt nur ein Dreieck mit stumpfem Winkel zu.
Und es ist per Zeichnung kein rechtwinkliges Dreieck möglich. 

---

Der Winkel 126,87° kann nicht in einem rechtwinkligen Dreieck liegen.

Bei den gesuchten Winkeln ist jeweils der Winkel zwischen \(\vec{a}\) und einem Richtungsvektor der jeweiligen Koordinatenachse in positiver Richtung gesucht. Die einfachsten RV sind

[1, 0] bei der x-Achse und [0, 1] bei der y-Achse.

Natürlich kannst du auch einfach nach dem Bild von Werner  36,8°  + 90°= 126,87° rechnen.

Das gilt hier in der Ebene. Die von dir benutzte Formel gilt aber (später) genau so auch mit Vektoren im Raum. Und dann sind die Überlegungen mit rechtwinkligen Dreiecken komplizierter.

---

Vielen Dank Wolfgang ! Ich werde mich noch weiter einlesen müssen, ich werde heute nicht sehr viel schlauer werden.

---

Ich muss mich weiter ins Schulbuch vertiefen und dann sehe ich solche sachverhalte vielleicht eher, auch wieso der einfachste RV in der Ebene die x-Achse und die y-Achse ist, und wieso die y-Achse 0,1 ist und wieso die x-Achse 1,0 ist.

Vielen Dank aber dir, auch deine Hilfe schätze ich immer !

---

[1, 0] ist der Vektor mit dem Pfeil von (0,0) nach (0,1) , und der verläuft doch in Richtung der x-Achse. Also ist er ein Richtungsvektor der x-Achse (analog y-Achse)

Und genau solche  Richtungsvektoren werden in deiner Formel verwendet, um Winkel zwischen einem Vektor \(\vec{a}\) und irgendwelchen Geraden (z.B. den Koordinatenachsen) zu berechnen.

---

Ok ich hab die Konstruktion verstanden. Aber nicht wieso ich eine Einheit 1 wähle. 

Ich verbinde den Ursprung mit dem Punkt X bzw. den Ursprung mit Punkt Y. Und bestimme deren Richtungsvektor indem ich den Punkt (0I0) von X (und Y) subtrahiere..  

Hätte ich das alleine machen müssen, hätte ich den Punkt X bei X(4I0) gewählt....
Ich wäre nicht drauf gekommen dass ich einfach sagen kann, ok der Punkt X liegt bei 1 oder der RV x hat die länge 1..

However, werde mich weiter einlesen müssen. Danke viel mal !

Richtungsvektor x

Richtungsvektor y