Klausurstress. Nullstellen von rationalen Funktionen: Bsp. f(x)=x^3(x+5)^2(x-3), f(x)=1/4 x^4 - 13/2 x^2 + 18

Question

Klausurstress und Angst 

Leute ich weiß nicht wie man es berechnet a b und c und wie gebe ich sowas an könnt ihr mir bitte bitte helfen.

Comments

Gehe mal auf diese Seite und gib die Funktionen ein. Schau bei "Erläuterung des Lösungsweg" die einzelnen Rechenschritte an.

Answer 1

Ohne Substitution lösen:

\(x^4 - 26  \cdot  x^2 + 72 = 0\)

\(x^4 - 26 \cdot x^2 = -72\)

\(x^4 - 26 \cdot x^2 +(\frac{26}{2})^2= -72+(\frac{26}{2})^2\)

\((x^2 -13)^2=97  |±\sqrt{~~}\)

1.)

\(x^2 -13=\sqrt{97}  \)

\(x^2 =13+\sqrt{97} |±\sqrt{~~}  \)

\(x_1 =\sqrt{13+\sqrt{97} } \)

\(x_2 =-\sqrt{13+\sqrt{97} } \)

2.)

\(x^2 -13=-\sqrt{97}  \)

\(x^2 =13-\sqrt{97}|±\sqrt{~~}  \)

\(x_3 =\sqrt{13-\sqrt{97}}  \)

\(x_4 =-\sqrt{13-\sqrt{97}}  \)

c)

Polynom in Linearfaktorenform:

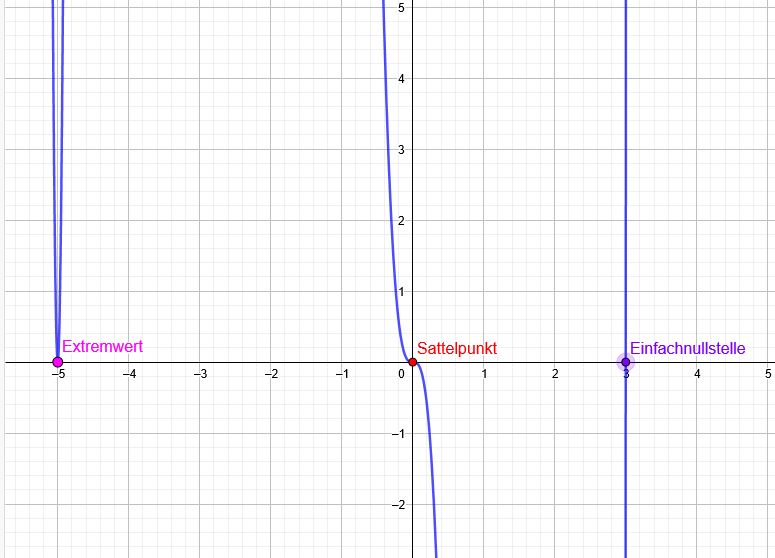
\(f(x)=x^3 \cdot (x+5)^2 \cdot(x-3)\)

\(x^3 \cdot (x+5)^2 \cdot(x-3)=0\)

Satz vom Nullprodukt:

1.) \(x^3 =0\)

\(x =0\) Hier ist eine dreifache Nullstelle ( Sattelpunkt oder Terrassenpunkt)

2.) \( (x+5)^2 =0\)

\(x=-5 \)  Hier ist eine zweifache Nullstelle (Extremwert)

3.)\((x-3)=0\)

\(x=3\)  Hier ist eine einfache Nullstelle

Answer 2

Hallo jf,

Nullstellen:

f(x) = 1/4x⁴ - 13/2 x² + 18 = 0   | * 4

x⁴ - 26x² + 72  =  0

Solche "biquadratischen" Gleichungen (es kommt nur x⁴ und x² vor) kann man auf eine quadratische Gleichung zurückführen:

Setze z = x²

z² - 26z + 72 = 0

z² + pz + q = 0

pq-Formel:  p = -26 ; q = 72

z_1,2 = - p/2 ± \(\sqrt{(p/2)^2 - q}\)  

.....

 z₁ = √97 + 13   ≈ 22,85

 z₂ = 13 - √97  ≈  3,15

Substitution rückgängig machen:

x = ± √z :           (beide z-Werte sind positiv!)

x_1,2  ≈  ± √(22,85)  ≈  ± 4,78     [ genaue Werte: ± √(√97 + 13 ) ]

x_3,4  ≈  ±√(3,15)  ≈  ± 1,755      [ genaue Werte: ± √(13 - √97) ]

Gruß Wolfgang

Answer 3

Hier drei Dinge die dir helfen die meisten Gleichungen in der Schule zu lösen.

1. Direktes Auflösen. Das gilt für alle Gleichungen in denen das x nur an einer Stelle auftritt.

2. Satz vom Nullprodukt. Ist ein Produkt mehrerer Faktoren null muss mind. ein Faktor null sein. Hier kann man jeden Faktor getrennt gleich null setzen.

3. VAMPS. Unter den kleinen Vampierchen fasse ich noch günstige Hilfsmittel zusammen.

V - Satz von Vieta
A - Ausklammern
M - Mitternachtsformel oder pq-Formel
P - Polynomdivision oder Horner-Schema
S - Substitution

Bei der umrandeten biquadratischen Gleichung hilft die Substitution

1/4*x^4 - 13/2*x^2 + 18 = 0

x^4 - 26*x^2 + 72 = 0

Subst. z = x^2

z^2 - 26*z + 72 = 0

z = 13 ± √97

x = ± √(13 ± √97)

x = ± 1.775
x = ± 4.780

Comments

Bei b) benutze Polynomdivision oder das Horner Schema um eine geratene Nullstelle auszuklammern. Diese Aufgabe gehört allerdings zu den Leichtesten. Du kannst alle Nullstellen mit x = 3 ∨ x = 2 ∨ x = -1 finden. Damit brauchst du nicht mal eine Polynomdivision machen. Du kannst es aber machen um dem Lehrer zu zeigen das du es zur Not auch könntest.

Bei c) benutze den Satz vom Nullprodukt.