gebrochenrationale Funktion, Kurvendiskussion, andere Ergebnisse als im Lösungsskript:( g(x)=(2x^4)/(x^4+1)

Question

bin dabei folgende Aufgabe zu lösen und habe 2 Fragen dazu.

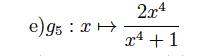
Lösung vom Lehrer:

 

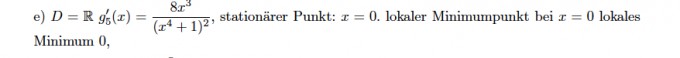
Ich verstehe die Lösung "lokaler Minimumpunkt bei x = 0 lokales Minimum 0" nicht, denn ich habe errechnet:

                                    8x²* (3-5x⁴)

      f''(x)=              __________________                     I  Extremstelle E x=0 einsetzen

                                        (x⁴+1)³

⇔ f''(0)=                  0                                                     I ? gilt hier nicht, die Regel, dass für ein Max/Min f''(E)</>0 sein muss? 

dann würde es ja hier kein Max/ Min geben, oder?

und:

Wenn

lim x↦+∞=2

lim x↦-∞=2, dann müsste doch bei (0/0) zumindest ein globales Minimum sein, weil es keine niedrigeren Funktionswerte als 0 gibt, oder?

wahrscheinlich habe ich total ein Gesetz missachtet und verrechnet ?:D

Würde mich über HIlfe freuen.

gebrochenrationale Funktion, Kurvendiskussion, andere Ergebnisse als im Lösungsskript:( g(x)=(2x^4)/(x^4+1)

Comments

Tipp: Kontrolliere Ergebnisse immer zumindest mit einem Plotter z.B. https://www.matheretter.de/rechner/plotlux oder mit

https://www.wolframalpha.com/input/?i=g(x)%3D(2x%5E4)%2F(x%5E4%2B1)  

Dann weisst du schon mal, ob du den Fehler bei deinen Rechnungen oder im Lösungsbuch suchen musst. 

Answer 1

Die hinreichende Bedingung besagt nicht das es wenn die zweite Ableitung gleich 0 ist kein Extremum gibt. 

Beispiel

f(x) = x^4 hat ein Minimum bei x = 0 obwohl die 2. Ableitung dort Null ist. Du kannst direkt mit den Funktionswerten der Ableitung argumentieren

f'(x) < 0 für x < 0 

f'(x) > 0 für x > 0 

Damit muss die Funktion dort ein Minimum haben.

Comments

Sorry,

ich bin leider nur ein Leihe hier:)

Wie genau kann ich denn mit den funktionswerten argumentieren?

wie argumentiere ich für meine Funktion von oben, dass es sich um ein Min handelt?

Durch einsetzen von x werten nahe an ±∞?

PS

bei der Aufgabe, die ich gestellt hatte, müsste dann doch der Punkt (0/0) ein globales Minimum sein und nicht ein lokales oder?

Der Rechner gibt es auch als globales an:)

---

Ein globales Minimum ist immer auch irgendwo ein lokales Minimum. Aber nicht jedes lokale Minimum ist auch ein globales Minimum. 

---

Vor x = 0 fällt der Graph wegen f'(x) < 0

Nach x = 0 steigt der Graph wegen f'(x) > 0

damit ist bei x = 0 ein Tiefpunkt.

Das ganze nennt man auch Vorzeichenwechselkriterium.

(0|0) ist ein lokales und auch ein globales Minimum.

---

ah soo!

vielen Dank!!