Dreieck maximaler Flächeninhalt

Question

Frage hab ich mir mal selber ausgedacht ...........

 

Wie errechne ich das größtmöglichste Rechteck welches in das Dreieck der folgenden Daten passt !

 

Answer 1

Hallo Element95, 

schöne Aufgabe!

Mal sehen, ob ich auch eine schöne Lösung finde :-)

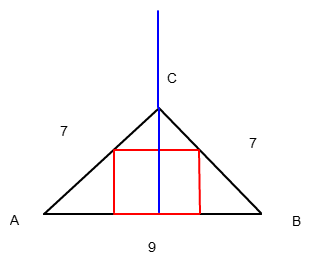
Ich platziere das gleichschenklige Dreieck so, dass die Seite a auf der x-Achse liegt und der Punkt C auf der y-Achse.

Dann hat A den Wert (-4,5|0), und B hat den Wert (4,5|0).

Mit Pythagoras erhalten wir den Punkt C:

4,5² + h² = 7²

h² = 7² - 4,5² = 28,75

h ≈ 5,3619

Also hat C den Wert (0|5,3619)

Wir erhalten für c, also die Strecke von C nach B die Geradengleichung

y = f(x) = mx + b

f(x) = mx + 5,3619

f(x) = -5,3619/4,5 * x + 5,3619

Jetzt betrachten wir wegen der Symmetrie des Dreiecks nur das halbe rote Rechteck links. 

Wir bekommen wir es maximal?

Das halbe Rechteck hat die Breite x und die Höhe f(x) und damit die Fläche

g(x) = x * [ (-5,3619/4,5) * x + 5,3619 ]

-5,3619/4,5 * x² + 5,3619 * x

Nun das Extremum suchen mithilfe der 1. Ableitung

g'(x) = 2 * (-5,3619/4,5) * x + 5,3619 = 0

2 * (-5,3619/4,5) * x = -5,3619

x = -5,3619 / 2 / (-5,3619/4,5) = 2,25

Also hat das gesamte maximale Rechteck die linke untere Ecke (-2,25|0) und die rechte untere Ecke (+2,25|0).

Die entsprechenden y-Werte ergeben sich für die rechte Hälfte des Rechtecks aus f(x), bei der linke Hälfte muss man darauf achten, dass dort die Funktion einen positiven Anstieg hat. 

Ich erspare mir jetzt aber die Berechnung der y-Werte und der Fläche des Rechtecks :-)

Besten Gruß

Comments

gut aber das geht ja nur wegen gleichschenklichkeit , wie wäre das bei einem ganz beliebigen Dreieck ?

---

Ich denke, das wäre ungleich schwieriger. Ich würde das Dreieck genauso platzieren wie oben, müsste dann aber berücksichtigen, dass die beiden Seiten des Dreiecks durch ganz verschiedene Geradengleichungen beschrieben würden. 

Wir hätten dann die Seite c links der y-Achse beschrieben durch die Geradengleichung f(x) und die Seite b rechts der y-Achse durch die Geradengleichung g(x). 

Dann müsste man das Maximum finden für das Rechteck

mit der Grundseite x₀ bis x₁ und der Höhe f(x₀); x₁ würde man dann so bestimmen, dass gilt:

g(x₁) = f(x₀)

Wie gesagt: Sicher machbar, aber schwieriger :-)

 

P.S.

Danke für den Stern :-D

---

ok danke für das fundierte Wissen :)

---

eins noch .... hättest du en ansatz dafür wenn das größtmöglichste Quadrat gesucht wird ?

---

Mh, beim - wie oben mittig platzierten - gleichschenkligen Dreieck wieder kein Problem. 

Wenn Du auf meine Skizze schaust, siehst Du, dass das eingezeichnete rote Rechteck fast ein Quadrat ist. Dann würde man die rechte x-Koordinate ganz einfach so bestimmen: 

f(x) = 2x

 

Idee für ein nicht gleichschenkliges Dreieck:

"Breite" des Quadrats = |x₀| + x₁

(Betragsstriche, weil x₀, die linke untere Ecke des Quadrats, laut unserer Skizze negativ ist)

"Höhe" des Quadrats= f(x₀) = g(x₁)