zu a)
y ' = (xy)/(1 +x^2)
dy/dx= (xy)/(1 +x^2)
dy/y=(x dx)/(1+ x^2)
ln|y|= 1/2 ln ( x^2+1) +C
|y| = √(x^2+1) * ± e^C
y = √(x^2+1) * C1
y= C1 *√(x^2+1)
zu b)
Ergebnis 1 mal ableiten und in die Aufgabe einsetzen.
Linke Seite muß = rechte Seite ergeben.
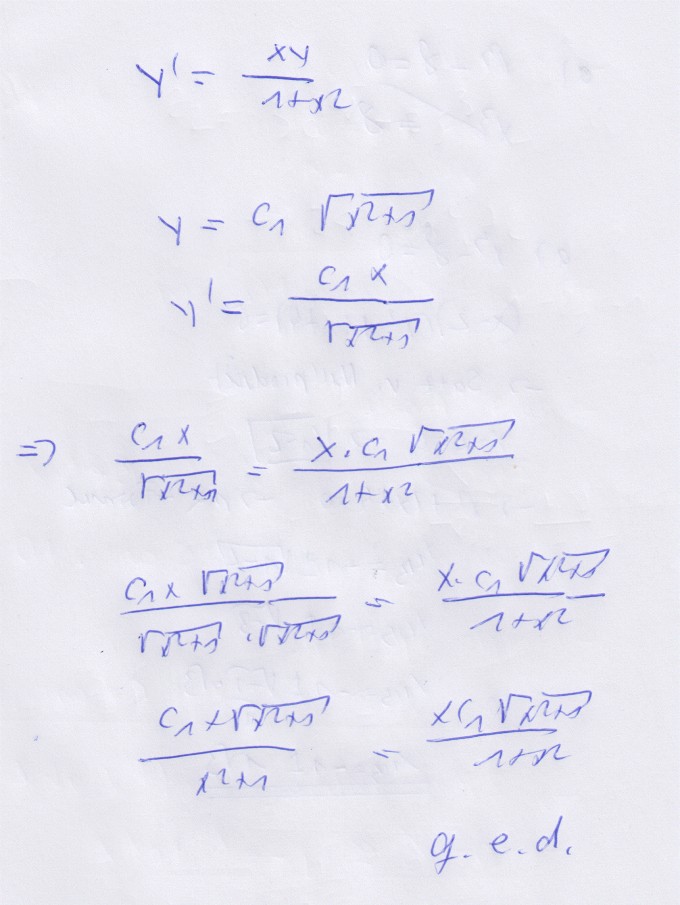
zu c)
y(1)=0
0=C_1 √2
C_1= 0
---->y=0
y(0)= -2
C_1= -2
---->y= -2 √(x^2+1)