Hallo jc,
K(x) = 1200 + 90x - 3x2 + 0,05x3
b) Bestimmen Sie die minimalen Grenzkosten
K'(x) = 90 - 6x + 0,15x2 = 0 (Grenzkosten)
K "(x) = 3·x/10 - 6 = 0 → x = 20 mit VZW - → +
K'(20) = 30 [€/Stück] → Grenzkostenminimum (20|30)
d) Bestimmen Sie das Betriebsoptimum (Minimum der Stückkosten)
Stückkosten k(x) = 1200/x + 90 - 3x + 0,05x2 (Unterscheidung K und k !)
k'(x) = x/10 - 1200/x2 - 3 ⇔ x3 /10 - 3x2 - 1200 = 0
Die Bezeichnung "Stück" legt nahe, dass xbmin ganzzahlig sein muss
k "(x) = 2400/x3 + 3/10 > 0 f.a. x>0 → k' ist linksgekrümmt
deshalb kann man mit einer Wertetabelle 38 < xbmin < 39 finden:
k(38) = 79.77894736 < k(39) = k(79.81923076)
Ansonsten bleibt nur:
Cardanoformeln oder Näherungsverfahren (z.B. Newtonverfahren)
→ x = (7000 - 4000·√3)1/3 + (4000·√3 + 7000)1/3 + 10
x ≈ 38,21640164
→ Betriebsoptimum (38 | 7977894736)
c) Bestimmen Sie das Betriebsminimum
falsche Teilantwort gelöscht (vgl. Kommentare)
e) Bestimmen Sie die totalen Stückkosten bei einer Produktion von 200 Stück.
k(200) = 1496 [GE / Stück ]
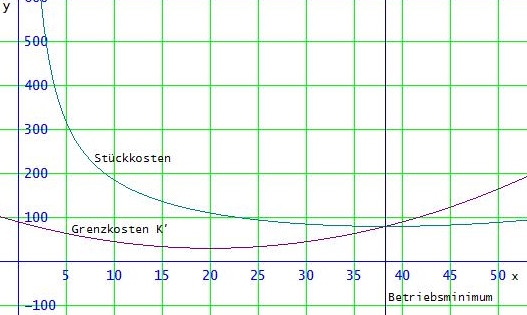
Im Bild muss es unten rechts "Betriebsoptimum "heißen.
Gruß Wolfgang