Abstand Gerade- Achse bestimmen

Question

Es handelt sich um folgende Aufgabe:

Berechnen Sie den Abstand der Geraden \( g: \vec{x}=\left(\begin{array}{c}{3} \\ {4} \\ {4}\end{array}\right)+t \cdot\left(\begin{array}{c}{0} \\ {1} \\ {0}\end{array}\right) \) von der \( x_{2} \) -Achse.

Die Bestimmung des Abstands zwischen Punkt und Geradeist mir klar, jedoch nicht zwischen Gerade und Achse.Kann ich zur Berechnung einen beliebigen Punkt wählen,welcher lediglich auf der x2-Achse liegt und mit diesem den Abstandbestimmen? Oder muss ich ganz anders vorgehen?Gruß myhealthyego

Answer 1

Hallo myhealthyego,

die Lage des Punktes  P(3|4|4)  der Geraden kann man durch einen Quader, dessen Kantenlängen die Koordinaten von P sind,  optisch veranschaulichen:

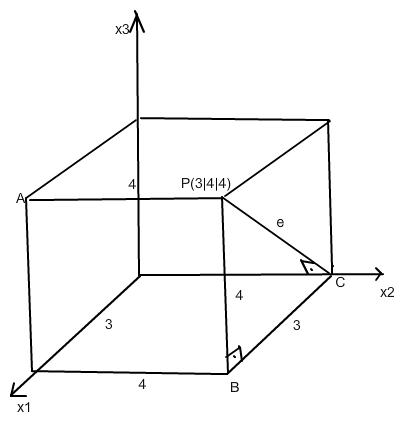
Deine Gerade verläuft durch A und P, weil sie mit dem Richtungsvektor [0,1,0]  zur x₂-Achse parallel ist.

e = PC ist der gesuchte Abstand.

Da  ΔBCP rechtwinklig ist,  gilt  e² = 4² + 3² = 25   →   e = 5   

Gruß Wolfgang

Comments

Danke für die gute Veranschaulichung!:)

Answer 2

Deine Gerade und die Achse sind parallel.  Du kannst also irgendeinen Punkt von g

( etwa  ( 3 ; 4 ; 4 ) ) nehmen und dessen Abstand zur x2-Achse bestimmen.

Comments

Sehe ich durch den Richtungsvektor u, dass sie parallel sein müssen?

---

So ist es, du kannst dir ja mal das Bild in meiner Antwort ansehen.

Answer 3

(3;4;4)·(0;1;0)/|(3;4;4)|=4/√41≈0,625 (Bitte in Spaltenschreibweise umschreiben). Leider falsch.

Comments

> Leider falsch.  

Dann kann man das einfach zu einem Kommentar machen und löschen.