Funktionsgleichung einer ganzrationalen Funktion dritten Grades mit 3 Bedingungen aufstellen?

Question

Ich soll eine Funktionsgleichung einer ganzrationalen Funktion dritten Grades aufstellen.

geg.sind die Bedingungen:

- P (2;0)

- Q (0;4)

- im Punkt R (1;f(1)) existiert ein Wendepunkt

die Normalform ist ja: f(x) = ax³ + bx² + cx + d

Wäre der nächste Schritt f(1) = a•1³ + b•1² + c•1 + d ?

Wie geht es dann weiter ?

Answer 1

Angaben

f(x) = ax³ + bx² + cx + d
f ´( x ) = 3 * a * x^2 + 2 * b * x + c
f ´´ ( x ) = 6 * a * x + 2 * b

- P (2;0)

- Q (0;4)

- im Punkt R (1;f(1)) existiert ein Wendepunkt

f ( 2 ) = 0
f ( 0 ) = 4
f ´´ ( 1 ) = 0

Es fehlt eine Angabe.
Bitte wenn möglich ein Foto der Aufgabe einstellen
oder den haargenauen Fragetext.

Comments

Die Komplette Aufgabe lautet:

Stellen Sie die Funktionsgleichung der ganzrationalen Funktion dritten Grades auf, die folgenden Bedingungen genügt:

- der Graf der Funktion berührt die x-Achse in Punkt P (2;0)

- die y-Achse wird im Punkt Q (0;4) geschnitten

- im Punkt R(1;f(1)) existiert ein Wendepunkt.

Skizzieren Sie den Grafen in ein Kartesisches Koordinatensystem. 

Zudem bin ich auch der Überzeugung das etwas fehlt, wir haben immer 4 Vorgaben erhalten.

---

- der Graf der Funktion berührt die x-Achse in
Punkt P (2;0)

Da haben wir es schon

Das Wort berühren zeigt an

f ´ ( 2 ) = 0
zusammen mit
f ( 2 ) = 0
f ( 0 ) = 4
f ´´ ( 1 ) = 0

kann die Aufgabe gelöst werden.

Kommst du damit klar ?

---

12a + 4b + c = 0
8a + 4b + 2c + d = 0
d = 4
6a + 2b = 0

f ( x ) = x^3 - 3·x^2 + 4

---

Also ich kann dem nicht ganz folgen, wieso wird z.B. Punkt P in die erste Ableitung eingesetzt ?

Wie man auf d und 8a + 4b +2c + d kommt ist verstehe ich.

Die Antwort von Roland ist da verständlicher, ohne Ihnen jetzt auf den Schlips treten zu wollen.

---

Also ich kann dem nicht ganz folgen, wieso wird z.B.
Punkt P in die erste Ableitung eingesetzt ?

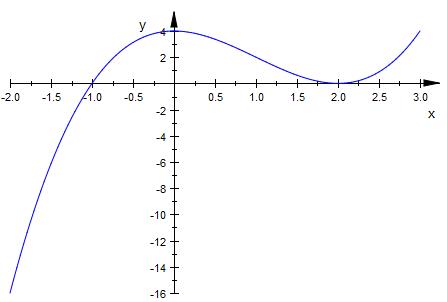
- der Graf der Funktion berührt die x-Achse in
Punkt P (2;0)

Der Punkt P ist ein Berührpunkt der Funktion
mit der x-Achse

Für Berührpunkte gilt
f ( x ) = g ( x )  | Koordinaten gleich
f ´( x ) = g ´( x )  | Steigung gleich

Die Steigung der x-Achse = 0

Also ist
f ´( 2 ) = 0
( siehe Skizze )

f ( x ) = ax³ + bx² + cx + d
f ´( x ) = 3 * a * x² + 2 * b * x + c
f ´´ ( x ) = 6 * a * x + 2 * b

f ( 2 ) = 0
f ´( 2 ) = 0 
f ( 0 ) = 4
f ´´ ( 1 ) = 0

Einsetzen
f ( 2 ) =  a *2³ + b *2² + c *2  + d = 0
f ´( 2 ) = 3 * a * 2² + 2 * b * 2 + c  = 0 
f ( 0 ) =  a * 0³ + b * 0² + c * 0  + d = 4
f ´´ ( 1 ) = 6 * a * 1 + 2 * b  = 0

Gleichungen
8 * a + 4 * b  + 2 * c   + d = 0
12 * a  + 4 * b  + c  = 0 
d = 4
6 * a  + 2 * b = 0

Du kannst gern weiterfragen bis die Aufgabe
auch für dich geklärt ist.

mfg Georg

---

Aaahh das mit den Berührungspunkten war mir nicht klar, danke!

Und wie kommt man jetzt auf diese Funktionsgleichung ?  f (x) = x³ - 3·x² + 4 

Ich weiß, dass d = 4 ist aber woher kommt der Rest ? Was ist mit a, b und c passiert ?

Bisher war es aber sehr Aufschlussreiche :)

---

12a + 4b + c = 0
8a + 4b + 2c + d = 0
d = 4
6a + 2b = 0

Das Ganze nennt man ein lineares
Gleichungssystem mit 4 Gleichungen
mit 4 Unbekannten.
Das muß man zur Beantwortung der
Ausgangsfrage lösen können.
Gauß, Einsetzungsverfahren usw.

12a + 4b + c = 0
8a + 4b + 2c + 4 = 0
6a + 2b = 0

12a + 4b + c = 0
c = -12a - 4b

Einsetzen
8a + 4b + 2 * ( -12a - 4b ) + 4 = 0
-16a - 4b = -4
-4a -  b  = -1
b = 1 - 4a

6a + 2b = 0
6a + 2 * ( 1 -4a ) = 0
6a + 2 - 8a = 0
-2a = -2
a = 1

b = 1 - 4a
b = -3

c = -12a - 4b
c = -12*1 - 4*(-3)
c = 0

Answer 2

Der Ansatz f(x) = ax³ + bx² + cx + d ist richtig.

P (2;0) führt zu 0=8a+4b+2c+d

Q (0;4) führt zu 4=d

- im Punkt R (1;f(1)) existiert ein Wendepunkt bedeutet f ''(1)=0, also f ''(x)= 6ax+2b und dann 0=6a+2b

Jetzt hast du 3 Gleichungen mit vier Unbekannten

(1) 0=8a+4b+2c+d

(2) d=4

(3) 0=6a+2b

Wenn du dich entschließt, alle Koeffizienten durch a auszudrücken ist b=-3a und es gilt 0=8a-12a+2c+4 und folglich c=2a-2 und du erhältst die Gleichung einer Kurvenschaar f_a(x) = ax³ - 3ax² + (2a-2)x +4.

Comments

Soweit habe ich es verstanden, für was steht das a bei f_a ?

f_a(x) = ax³ - 3ax² + (2a-2)x +4 das ist die Fertige Funktionsgleichung ? 

Muss man nicht alle Buchstaben sprich jetzt noch a ausschließen ?

---

Georgborn hat dir ja schon ausführlich geantwortet. Ich konnte nicht wissen, dass (2/0) ein Berührpunkt der x-Achse sein soll. Dann kann man auch eine vierte Gleichung aufstellen und a bestimmen. f_a ist Bezeichnung für eine Funktionenschar (hattet ihr wohl noch nicht?)

---

Hallo Roland,

das der Punkt P ein Berührpunkt war konnte
niemand aus der ersten Aufgabenstellung
ersehen.

Die mathematische Sprache ist mitunter
wesentlich genauer als die Alltagssprache
sodaß  diese Information vom Fragesteller
halt übersehen wurde.

---

Hallo Georg, und woher hast du diese Information?

Ich bin immer wieder erstaunt, wie Beantworter im Forum die vom FS weggelassenen Informationen erraten. Wenn ich das selbst  versuche, fliegt es mir anschließend um die Ohren.

---

4 Unbekannte in 3 Gleichungen das kann nach
Adam Riese nichts geben.

Möglichkeiten
- Berechnung einer Kurvenschar.
  Ist meist zu kompliziert. Eher unwahrscheinlich.

- Nachfrage ob vielleicht eine Information
nicht angegeben wurde. Wahrscheinlicher.

Die 2 größten Mißverständnisse zwischen den
Fragestellern und den Antwortgebern sind

- fehlende Klammerung

- es wurden Information weggelassen
oder
- es erfolgte bereits eine eigenwillige Inter-
pretation der Frage durch den  Fragesteller.
Diese Fälle können durch Einstellung des
Originalfragetextes oder Fotos geklärt
werden.