Eine Linearkombination bedeutet, einen Vektor - hier \(\vec{OS}\) als eine Summe von anderen Vektoren darzustellen, wobei jeder der anderen mit einem Faktor multipliziert wird. In diesem Fall
$$\vec{OS}=x\cdot \vec{OA} + y\cdot \vec{OB} + z\cdot \vec{OC}$$
\(x\), \(y\) und \(z\) sind die Faktoren, mit denen die Vektoren multipliziert werden. Und nach denen ist gefragt. ich nehme jetzt mal das Ergebnis vorweg. Du solltest bereits heraus bekommen haben, dass \(\vec{AS}=\frac{1}{3} (\vec{a}+\vec{b})\) ist, wenn \(\vec{a}=\vec{AB}\) und \(\vec{b}=\vec{AC}\) sein soll, wie beim letzten Mal.
Und jedes Seite im Dreieck ist die Differenz der beiden Ortsvektoren der begrenzenden Ecken - also ist
$$\vec{a}=\vec{AC}=\vec{OC}-\vec{OA} \quad \text{und} \space \vec{b}=\vec{AB}=\vec{OB}-\vec{OA}$$
Und der Ortsvektor zum Schwerpunkt \(S\) ist \(\vec{OS}=\vec{OA}+\vec{AS}\). Und noch ein Bild zur Orientierung:
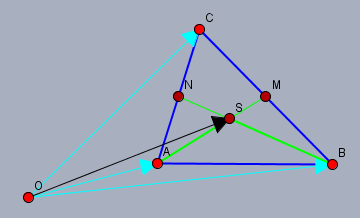
Jetzt muss man das nur noch einsetzen:
$$\vec{OS}=\vec{OA}+\vec{AS}=\vec{OA}+\frac{1}{3} (\vec{a}+\vec{b})=\vec{OA}+\frac{1}{3} (\vec{OC}-\vec{OA}+\vec{OB}-\vec{OA})$$
$$\space =\vec{OA}+\frac{1}{3} \vec{OC}-\frac{1}{3} \vec{OA}+\frac{1}{3} \vec{OB}-\frac{1}{3} \vec{OA}=\frac{1}{3}\vec{OA} + \frac{1}{3} \vec{OB} + \frac{1}{3} \vec{OC}$$
Falls Dir nicht klar ist, wie ich auf \(\vec{AS}=\frac{1}{3} (\vec{a}+\vec{b})\) komme, oder noch was anderes unklar ist, so frage bitte nach.
Gruß Werner