Man mache sich zunächst mal eine Zeichnung
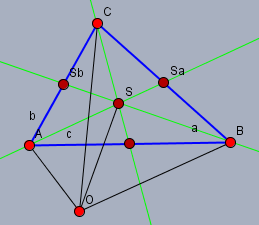
und um die Schreibarbeit abzukürzen sei \(\vec{AB}=c\) und \(\vec{BC}=a\). Das Verhältnis \(AS:AS_a=r\) und \(BS:BS_b=s\). Dann ist
$$c+ \vec{BS}=\vec{AS}$$
$$c+ s \cdot \vec{BS_b}= r \cdot \vec{AS_a}$$
$$c+ s \cdot (-c+\frac{1}{2}(c+a))= r \cdot (c+\frac{1}{2}a)$$
$$c -\frac{s}{2}c+\frac{s}{2}a= r \cdot c+\frac{r}{2}a$$
$$c(1 -\frac{s}{2} - r)+a(\frac{s}{2}-\frac{r}{2})=0$$
und das ist genau dann richtig, wenn die Faktoren vor den Vektoren =0 sind. Daraus folgt \(s=r=\frac{2}{3}\)
weiter ist $$\vec{OS}=\vec{OA} + \frac{2}{3}\vec{AS_a}=\vec{OA} + \frac{2}{3}\left( \vec{AB} + \frac{1}{2}\vec{BC}\right) \\ = \vec{OA} + \frac{2}{3}\left( \vec{OB}-\vec{OA} + \frac{1}{2}(\vec{OC}-\vec{OB})\right) = \frac{1}{3}\vec{OA} + \frac{1}{3} \vec{OB} + \frac{1}{3}\vec{OC}$$
Falls noch Fragen offen sind, so melde Dich bitte.
Gruß Werner