Neigung bestimmen um gleiche Teilflächen zu haben. f(x)=x^2 mit den Integrationsgrenzen [0;5]

Question

Bsp.:

Geg.: f(x)=x² mit den Integrationsgrenzen [0;5].Durch den Punkt P(5/0) geht eine Gerade.Frage: Welche Neigung muss die Gerade haben, damit die Teilflächen gleich sind? Hinweis: Die Gerade schneidet die Funktion f(x)=x².
Meine Vermutung : Die Gerade muss einen Neigungswinkel von -45° haben also die Steigung -1 (tan-45°=k), damit man gleiche Teilflächen hat.
Liege ich falsch oder richtig
Würde mich auf eine Antwort freuen!

Comments

Skizze:

~plot~ x^2; x=0; x=5; -3(x-5); -2(x-5);[[-1| 6| -1| 30]] ~plot~ 

45° (Also f(x)=-(x-5).) wäre ein ziemlicher Zufall.  Die Kurve ist eine Parabel und kein Kreis. 

Kannst du integrieren? Überprüfe deine Vermutung mit Integration. 

Danach machst du eine allgemeine Rechnung mit g(x) = a (x-5) , wobei a< 0 und bestimmst a. 

Answer 1

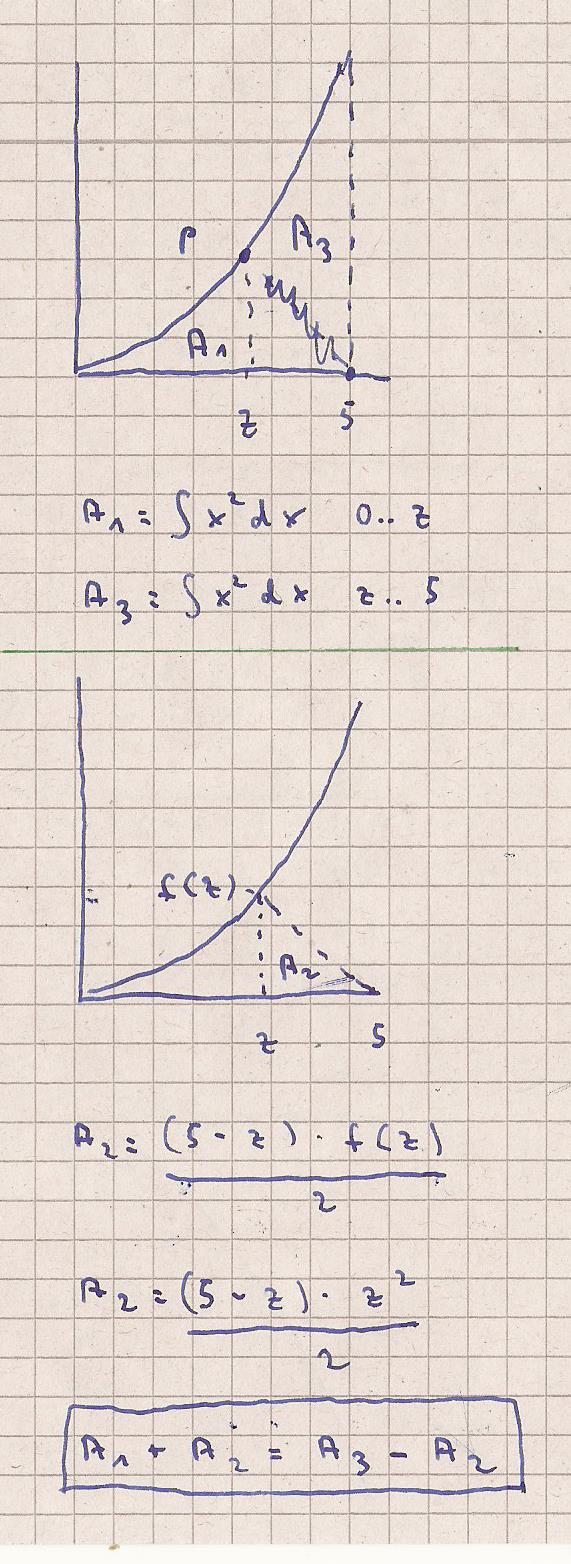
Allgemeiner Hinweis : eine Skizze ist
empfehlenswert

ich habe mein Matheprogramm rechnen
lassen. Eine algebraische Lösung gibt es nicht.

  

Berechnet werden kann mit dem Newton-Verfahren.

Der Graph
- blaue Kurve a1 + a2
- rote Kurve a3 - a2

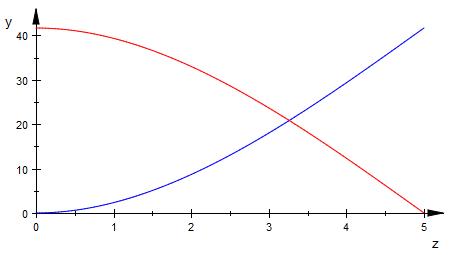
a1 + a2 = a3 - a2
z ungefähr 3.3

Kannst du Integralrechnung und das Newton Verfahren ?