Hallo bi,
6)
Lies die Steigung m und - wenn möglich - den y-Achsenabschnitt n aus der Grafik ab. Setze beides dann in y = m·x + n ein.
Beispiele:
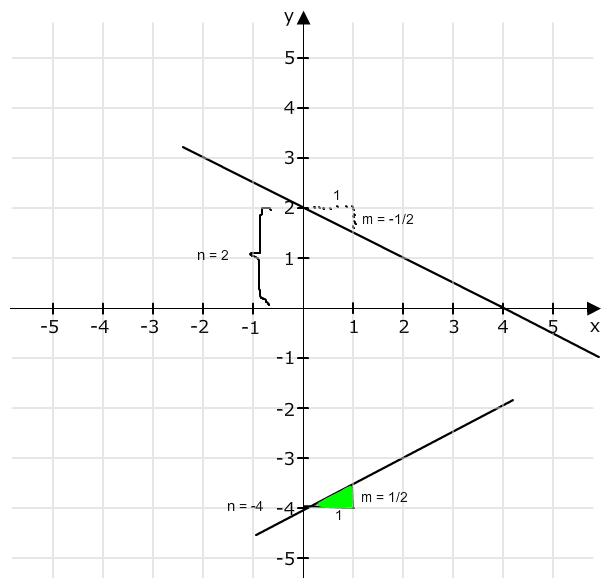
Wenn n in der Grafik nicht ablesbar ist ( z.B. bei c)), kannst du in die Gleichung y = m * x + n die Koordinaten eines beliebigen abgelesenen Punktes und m einsetzen. Dann kannst du n ausrechnen.
7)
Die Gerade durch die Punkte P1( x1 | y1 ) und P2( x2 | y2 ) hat die Gleichung
y = (y2 -y1) / (x2 - x1) • ( x - x1 ) + y1 [ 2 Punkte--Formel ]
Du bei jeder Aufgabe zwei Punkte der Geraden gegeben. Deren Koordinaten in die Gleichung einsetzen, dann Klammer auflösen und zusammenfassen → Geradengleichung
Jetzt kannst du bei den übrigen Punkten jeweils die gegebene Koordinate in die Geradengleichung einsetzen und die fehlende Koordinate ausrechnen.
Beispiel 7a) (2|5) , (5|9) , .... , ( ? | -2 )
Geradengleichung:
y = (9-5) / (5-2) * (x - 2) + 5 = 4/3 * (x - 2) + 5 = 4/3 * x - 8/3 + 5 = 4/3 * x + 7/3
-2 = 4/3 * x + 7/3 | - 7/3
-13/3 = 4/3 * x | : 4/3
-13/3 * 3/4 = x
-13/4 = x → die fehlende x-Koordinate ist -13/4
Gruß Wolfgang