Wie kann man bei der folgenden Funktion Stetigkeit zeigen und Beweisen? f(x) = (√(1+x) - 1)/x

Question

$$f(x) = \frac {\sqrt {1+x} -1} {x} $$

Ich hab mit  $$ \sqrt {1+x} +1$$ erweitert und habe dann am Ende mittels der Regel
von L`Hospital und Lim
$$ \frac {1} {\sqrt{ \frac{1}{x} + 1}}$$

ist das korrekt?

 f(x) = (√(1+x) - 1)/x

Comments

$$f(x) = \frac {\sqrt {1+x} -1} {x} $$

das natürlich...

---

EDIT: Habe das f(x) in der Frage mit dem in deinem Kommentar ausgetauscht.

Du berechnest gerade den ersten Grenzwert hier:

https://www.wolframalpha.com/input/?i=limes+(%E2%88%9A(1%2Bx)+-+1)%2Fx 

?

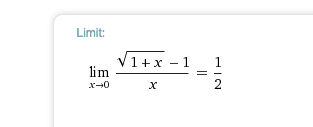
Vergleiche deine Zwischenresultate nun mit der alternate form im obigen Link.

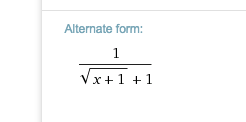
Dort kannst du direkt x=0 einsetzen.

Du hast dich also nochmals irgendwo verrechnet.

Vergiss nicht zu erwähnen, warum die Funktion im ganzen Definitionsbereich stetig ist.

Im Moment ist erst gezeigt, dass sie bei x=0 stetig ergänzt werden kann.

Achtung: Wolframalpha rechnet jeweils simultan noch mit komplexen Zahlen (Farbunterschied in den Graphen) Das ignorieren.