Gaußklammer Stetigkeit beweisen von: f:R -> R mit x -> ⎣x⎦+√(x-⎣x⎦)

Question

f:R -> R mit x -> ⎣x⎦+√(x-⎣x⎦)

ich weiß, dass die Funktion stetig ist. aber wie beweist man das? Das mit den gaußklammern seh ich zum ersten mal 

hätte da jemand eine Idee??

Answer 1

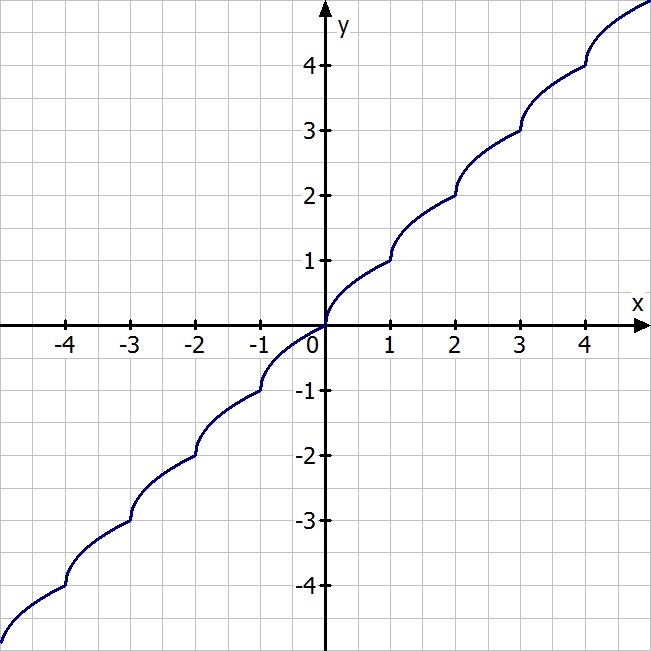
Betrachte nur mal die Gausklammerfunktion. An welchen Stellen vermutest du da die Unstetigkeitsstellen?

Also wenn unsere Funktion unstetig sein sollte dann auch an den Ganzzahligen Werten von x.

Also betrachte mal den Grenzwert ein 2 oder 3 ganzzahligen Werten. Und zwar sowohl den Rechtsseitigen als auch den Linksseitigen. Was stellst du fest.

Ich zeichne das noch mal.

Comments

ich hab ja nicht behauptet das es unstetig ist 

ich wusste das es stetig ist aber ich weiß nicht wie ich das beweisen soll formal 

es ist gleichmäßig stetig 

---

Stetig bedeutet das es für unendlich kleine änderungen von x auch unendlich kleine änderungen von y gibt.

Wie ist der linke und rechtsseitige Grenzwert an der Stelle x = 2. Kannst du das z.B. ausrechnen.

---

das hat ja nur einen linksseitigen Grenzwert