Guten Tag MatheLounge,
undzwar muss ich zurzeit beweisen, dass:

nachweisen muss nur wie?
Bsp. ich möchte zeigen, dass die gegebene Menge das Assoziativgesetz bzg. der Addition erfüllt, jedoch kann ich doch nicht das Kommutativgesetz, Neutrales Element sowie das Inverse Element anwenden, da diese ja auch nicht bewiesen sind oder?
Ich habe es so versucht:
(Beweis des Assoziativgesetzes bzg. der Addition)
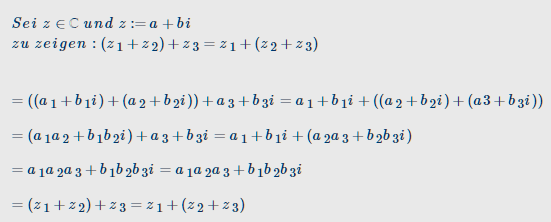
Oder ist mein Vorgehen falsch?
BlackFrost